��ϕ��@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����\�Ȋ�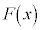 �������āA
�������āA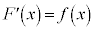 �C�܂�A
�C�܂�A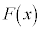 ��������
��������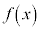 �C
�C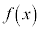 �̌��n����
�̌��n����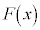 �ł���Ƃ��A
�ł���Ƃ��A
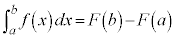 ���A
���A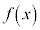 ��
��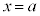 ����
����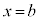 �܂ł���ϕ��ƌ����Ba�����[�Ab����[�ƌ����B
�܂ł���ϕ��ƌ����Ba�����[�Ab����[�ƌ����B
��ϕ��̌v�Z�̓r���ߒ��ň�U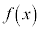 �̌��n����
�̌��n����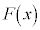 �ł��邱�Ƃ��������߂ɁA
�ł��邱�Ƃ��������߂ɁA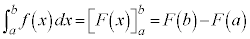 �̂悤�ɏ����B
�̂悤�ɏ����B
��ϕ��ɂ͈ȉ��̐���������B
(i) 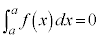
(ii) 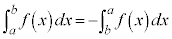
(iii) 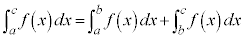
(iv) 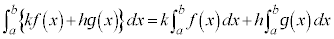
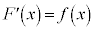 �C
�C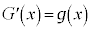 ���Ƃ��āA(i)�`(iv)�̏ؖ������Ă����܂��B
���Ƃ��āA(i)�`(iv)�̏ؖ������Ă����܂��B
(i) 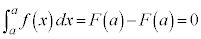
(ii) 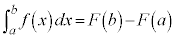 �C
�C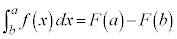 ���A
���A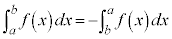
(iii) 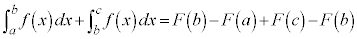
�@�@�@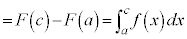
(iv) 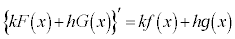 ���A
���A
�@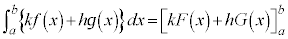
�@�@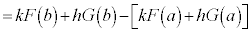
�@�@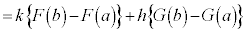
�@�@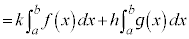
�s��ϕ��͊��ł����A��[�Ɖ��[���萔�Ȃ��ϕ��͒萔�ɂȂ�܂��B
��1�D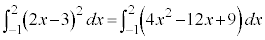
�@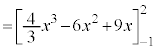
�@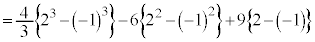
�@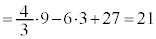
��2�D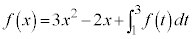 ������
������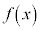 �����߂�B
�����߂�B
[��]�@�܂��A��ϕ���萔�Ƃ����܂��B
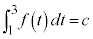 �@����@�@�Ƃ����āA
�@����@�@�Ƃ����āA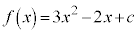 �@����A
�@����A
������@�ɑ������ƁA
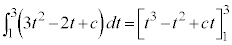
�@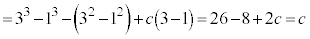
�� 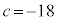
�A�ɑ�����āA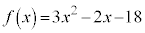 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B