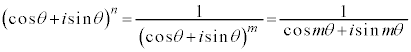ド・モアブルの定理 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
iを虚数単位、θを実数、nを整数として、
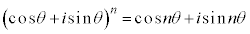･･･①
が成り立つ。
[証明] まず、nが自然数の場合について、数学的帰納法で証明する。
(Ⅰ)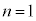 
のとき、①は成り立つ。
(Ⅱ)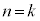 
のとき成り立つとして、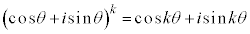
両辺に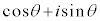
をかけて、
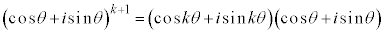
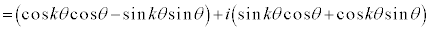
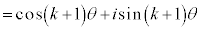
よって、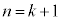
のときにも①は成り立つ。
(Ⅰ)，(Ⅱ)より、nが自然数のときには①は成り立つ。
(Ⅲ) nが負の整数のとき、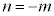
として、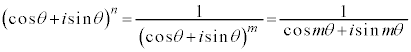
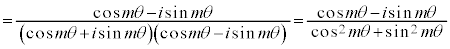(分母の実数化を行った)
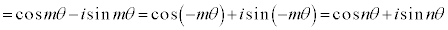
(Ⅳ)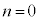 
のときは明らかに①は成り立つ。
(Ⅰ)～(Ⅳ)より、nを整数として、①が成り立つ。(証明終)
ド・モアブルの定理を、zを0でない複素数、nを整数として、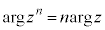
ということもできる(
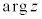はzの偏角)。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。