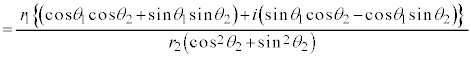�Ίp�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���f������������f��z�̕\���_P���Ƃ�Ƃ��A����OP�Ǝ���(x��)�̂Ȃ��pθ���Ίp�Ƃ���(�����v����Ίp�̐��̌����Ƃ���)�B
�@�@�@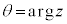
�ƕ\���B
�_P�̍��W��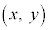 �Ƃ��āAz����Βl�F
�Ƃ��āAz����Βl�F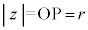 �Ƃ���ƁA
�Ƃ���ƁA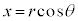 �C
�C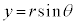 ���Az���Ɍ`���F
���Az���Ɍ`���F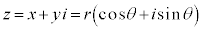 �̌`�ɕ\�����Ƃ��̊pθ���Ίp�ł���B
�̌`�ɕ\�����Ƃ��̊pθ���Ίp�ł���B
�Ίp�̐���
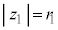 �C
�C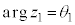 �C
�C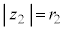 �C
�C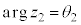 �Ƃ��āA
�Ƃ��āA
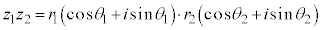
�@�@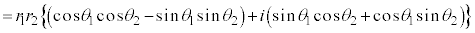
�@�@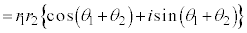
�����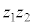 �̕Ίp��
�̕Ίp��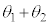 ���Ƃ������Ƃ�����A
���Ƃ������Ƃ�����A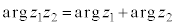 ����@ �����藧�B
����@ �����藧�B
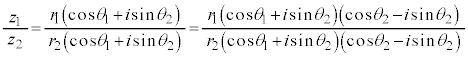 (����̎��������s����)
(����̎��������s����)
�@�@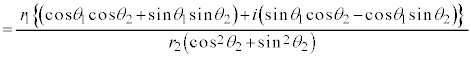
�@�@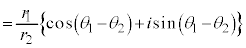
�����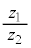 �̕Ίp��
�̕Ίp��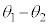 ���Ƃ������Ƃ�����A
���Ƃ������Ƃ�����A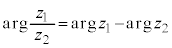 ����A �����藧�B
����A �����藧�B
�܂��A�h�E���A�u���̒藝���A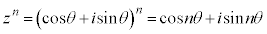
����́A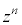 �̕Ίp��
�̕Ίp��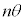 ���Ƃ������Ƃ�����A
���Ƃ������Ƃ�����A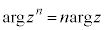 ����B �����藧�B
����B �����藧�B
�@�C�A�C�B�́A�Ίparg���ΐ�log�̂悤�Ȑ����������Ƃ������Ă���B
2�����̂Ȃ��p
�A�����A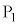 (
(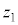 )�C
)�C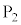 (
(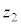 )�Ƃ��āA
)�Ƃ��āA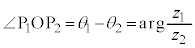 ������A
������A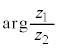 �͐���
�͐���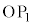 �Ɛ���
�Ɛ���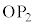 �̂Ȃ��p��\���Ă���B�����
�̂Ȃ��p��\���Ă���B�����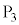 (
(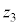 )�Ƃ��āA����
)�Ƃ��āA����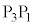 �Ɛ���
�Ɛ���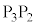 �̂Ȃ��pφ���A
�̂Ȃ��pφ���A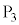 �����_�ɗ���悤�ɑS�̂�
�����_�ɗ���悤�ɑS�̂�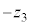 ���s�ړ����čl����A
���s�ړ����čl����A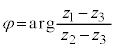 �ŗ^������B
�ŗ^������B
���D�Ίp�͖{����ʊp�ōl����Bn�𐮐��Ƃ��āA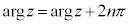 �ɒ��ӁB
�ɒ��ӁB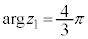 �C
�C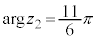 �Ƃ���ƁA
�Ƃ���ƁA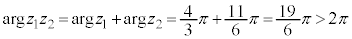 �ƂȂ邪�A
�ƂȂ邪�A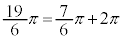 �Ȃ̂ŁA
�Ȃ̂ŁA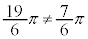 �ł����Ă��A
�ł����Ă��A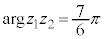 �Ƃ��Ă��������B
�Ƃ��Ă��������B
�܂��A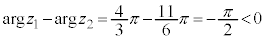 �ƂȂ邪�A
�ƂȂ邪�A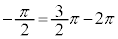 �Ȃ̂ŁA
�Ȃ̂ŁA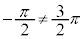 �ł����Ă��A
�ł����Ă��A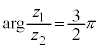 �Ƃ��Ă��������B
�Ƃ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 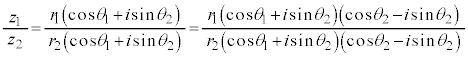 (����̎��������s����)
(����̎��������s����)