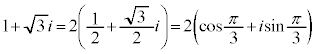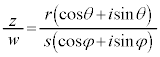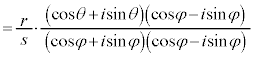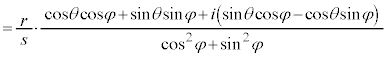�Ɍ`���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���f��������̌��_�ȊO�̓_P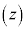 �ɂ��āA
�ɂ��āA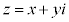 �Ƃ��A
�Ƃ��A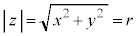 �C����OP�������̐������ƂȂ��p��θ �Ƃ���Ƃ��A
�C����OP�������̐������ƂȂ��p��θ �Ƃ���Ƃ��A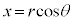 �C
�C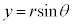 ���A
���A
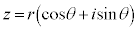
�Ə����܂��B���̌`���Ɍ`���ƌ����܂��Bθ��z���Ίp�ƌ����A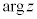 �Ə����܂��B
�Ə����܂��B
z�����f��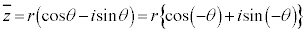 ���A���f���̕Ίp��
���A���f���̕Ίp��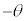 �ɂȂ�܂��B�܂�A
�ɂȂ�܂��B�܂�A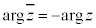 �ł��B
�ł��B
[��1]�@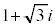 �̋Ɍ`���́A
�̋Ɍ`���́A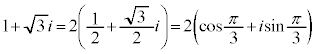
[��2]�@1) 1�̋Ɍ`���́A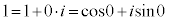
�@�@2) i�̋Ɍ`���́A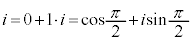
�@�@3) 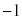 �̋Ɍ`���́A
�̋Ɍ`���́A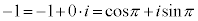
�@�@4) 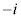 �̋Ɍ`���́A
�̋Ɍ`���́A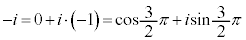
2�̕��f��z�Cw�̋Ɍ`�����A
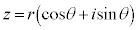
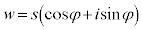
�Ƃ��܂��B
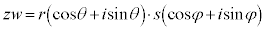
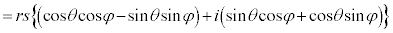
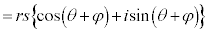
������A�Ɍ`����2�̕��f���̐ς��v�Z����ƁA��Βl�́A�e�X�̐�Βl�̐ςƂȂ�A�Ίp�́A�e�X�̕Ίp�̘a�ƂȂ邱�Ƃ��킩��܂��B�܂�A
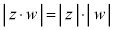
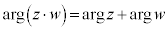 �@����@
�@����@
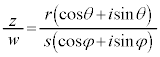
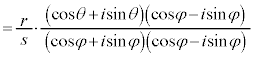
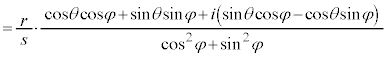
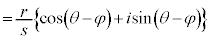
������A�Ɍ`����2�̕��f���̏����v�Z����ƁA��Βl�́A�e�X�̐�Βl�̏��ƂȂ�A�Ίp�́A�e�X�̕Ίp�̍��ƂȂ邱�Ƃ��킩��܂��B�܂�A
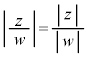
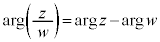 �@����A
�@����A
�@�C�A�����킹�āA���f���̕Ίparg�ɂ́A�ΐ�log�̂悤�Ȑ��������邱�Ƃ��킩��܂��B
���ہAn�����R���Ƃ��āA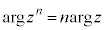 �����藧���܂�(�h�E���A�u���̒藝���Q��)�B
�����藧���܂�(�h�E���A�u���̒藝���Q��)�B
���f��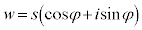 �ɁA���f��
�ɁA���f��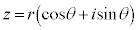 ��������ƁA
��������ƁA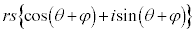 �ɂȂ�Ƃ������Ƃ́A���f��������ŁAw�̕\���_
�ɂȂ�Ƃ������Ƃ́A���f��������ŁAw�̕\���_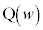 �Ɍ������x�N�g��
�Ɍ������x�N�g��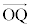 �̒�����
�̒�����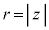 �{���āA
�{���āA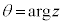 ������]����ƁA
������]����ƁA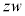 �̕\���_
�̕\���_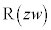 �Ɍ������x�N�g��
�Ɍ������x�N�g��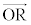 �ɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
�ɂȂ�A�Ƃ������Ƃ��Ӗ����Ă��܂��B
���f��z��������Ƃ������Ƃ́A���f�����ʏ�Ŋg��k���Ɖ�]���s���A�Ƃ������Ƃ�\���Ă���̂ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B