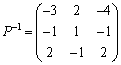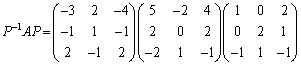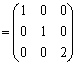行列の対角化 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
2次正方行列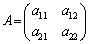 が2つのベクトル
が2つのベクトル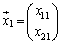 ,
,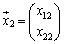 にかけられて、
にかけられて、
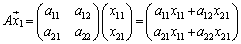 ・・・①
・・・①
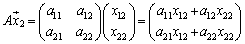 ・・・②
・・・②
という2式ができたとします。
この2式を1つの式にまとめる、という技巧があります。
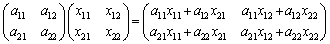
という行列の積の計算をよく眺めると、
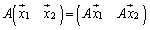 ・・・③
・・・③
という形をしていることがわかります。
同様に、2次正方行列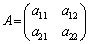 と、2つの実数
と、2つの実数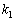 ,
,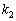 ,2つのベクトル
,2つのベクトル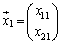 ,
,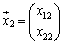 があるときに、
があるときに、
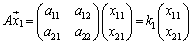
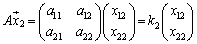
という2つの式を③を用いて1つにまとめることを考えます。
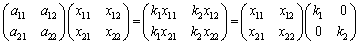
と書けるので、
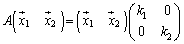 ・・・④
・・・④
と書くことができます。
n次正方行列Aが、相異なる固有値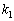 ,
,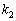 ,・・・,
,・・・,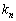 をもち、固有値
をもち、固有値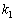 ,
,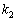 ,・・・,
,・・・,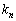 に対応する固有ベクトルが
に対応する固有ベクトルが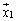 ,
,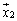 ,・・・,
,・・・,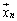 だとすると、
だとすると、
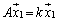 ,
,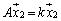 ,・・・,
,・・・,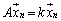
が成り立ちます。これらについても、④と全く同様にして、行列を用いて1つにまとめて表すことができます。
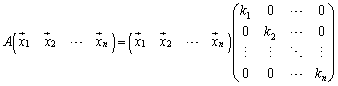 ・・・⑤
・・・⑤
行列Aの固有ベクトル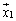 ,
,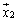 ,・・・,
,・・・,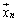 を横に並べてできる行列を
を横に並べてできる行列を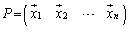 とすると、
とすると、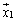 ,
,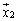 ,・・・,
,・・・,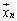 は1次独立(固有値・固有ベクトルを参照)なので、Pは逆行列
は1次独立(固有値・固有ベクトルを参照)なので、Pは逆行列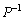 をもちます。⑤は、Pを用いて、
をもちます。⑤は、Pを用いて、
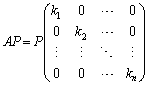
と書くことができます。ここで、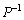 を左からかけると、
を左からかけると、
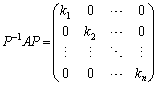
つまり、n次正方行列Aが相異なる固有値をもつときに、固有ベクトルを横に並べてできる行列をPとして、Aの左から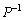 をかけ、Aの右からPをかけると、固有値が対角成分となりそれ以外の成分はすべて0であるような行列になります。この操作を行列の対角化と言います。
をかけ、Aの右からPをかけると、固有値が対角成分となりそれ以外の成分はすべて0であるような行列になります。この操作を行列の対角化と言います。
注.実は、固有方程式: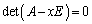 がl重解
がl重解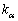 をもつ場合であっても、固有値
をもつ場合であっても、固有値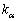 に対応する固有ベクトルがl個ある場合には、行列Aを対角化することができます。このときには、固有ベクトルを横に並べた行列をPとして、Aを対角化すると、
に対応する固有ベクトルがl個ある場合には、行列Aを対角化することができます。このときには、固有ベクトルを横に並べた行列をPとして、Aを対角化すると、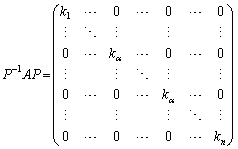 のように、対角成分に
のように、対角成分に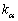 がl個並びます。
がl個並びます。
固有方程式: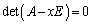 がl重解
がl重解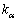 をもつ場合、固有値
をもつ場合、固有値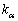 に対応する固有ベクトルがl個未満の場合には、行列Aを対角化することはできず、類似の操作を行うと、Jordanの標準形と呼ばれる形になります。
に対応する固有ベクトルがl個未満の場合には、行列Aを対角化することはできず、類似の操作を行うと、Jordanの標準形と呼ばれる形になります。
2次正方行列の場合では、固有方程式が重解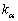 をもつと、
をもつと、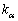 に対する固有ベクトルは1つしか存在せず、対角化することはできません。
に対する固有ベクトルは1つしか存在せず、対角化することはできません。
例1.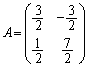 を対角化する。
を対角化する。
固有方程式は、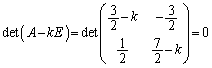 より、
より、
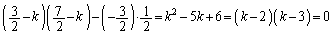
∴ 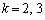
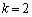 のとき、
のとき、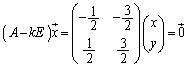
∴ 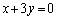
例えば、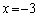 ,
,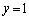
固有値2に対応する固有ベクトルは、tを実数として、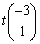
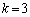 のとき、
のとき、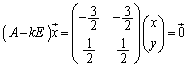
∴ 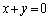
例えば、
固有値3に対応する固有ベクトルは、sを実数として、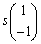
よって、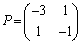 とすると、
とすると、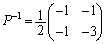
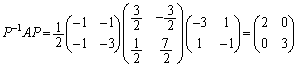
例2.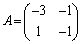 は、固有方程式が重解をもち対角化できない。
は、固有方程式が重解をもち対角化できない。
固有方程式は、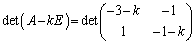
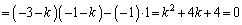
∴ 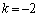
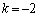 のとき、
のとき、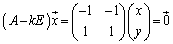
∴ 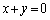
例えば、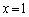 ,
,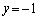
固有値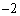 に対応する固有ベクトルは、tを実数として、
に対応する固有ベクトルは、tを実数として、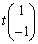
これ以外に固有ベクトルはありません。そこで、
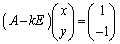 となるベクトルを考えます。
となるベクトルを考えます。
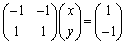
∴ 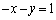
例えば、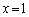 ,
,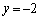
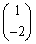 を固有ベクトルの代用として、
を固有ベクトルの代用として、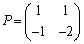 を考えます。
を考えます。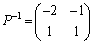
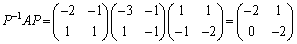
この形は、対角成分に固有値が重解なので2個並び、固有値が並んだ右側に1が来ている形で、Jordanの標準形と言われています。
なぜこういう形になるかと言うと、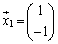 ,
,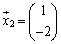 として、
として、
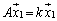 ,
,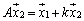 を1つにまとめて書くと、
を1つにまとめて書くと、
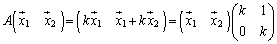
となるからです。
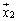 を
を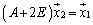 のようにとるのは、
のようにとるのは、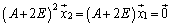 とするためです。
とするためです。
例3.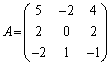 を対角化する。
を対角化する。
固有方程式は、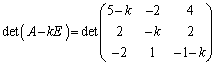

∴ 
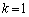 のとき、
のとき、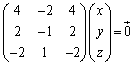
∴ 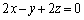
これを満たすのは、例えば、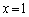 ,
,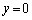 ,
,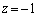 ,または、
,または、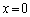 ,
,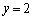 ,
,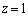
よって、固有値1に対応する固有ベクトルは、 ,
,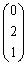
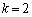 のとき、
のとき、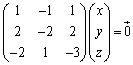
∴ 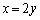 ,
,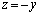
これを満たすのは、例えば、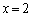 ,
,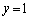 ,
,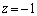
よって、固有値2に対応する固有ベクトルは、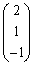
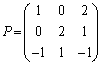 とすると、
とすると、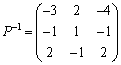
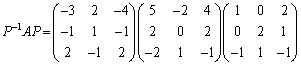
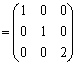
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 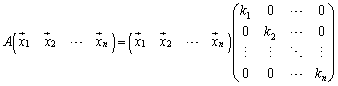 ・・・⑤
・・・⑤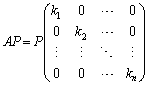
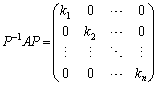
 のように、対角成分に
のように、対角成分に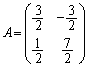 を対角化する。
を対角化する。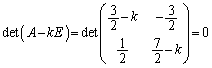 より、
より、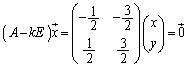
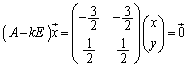
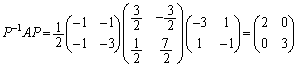
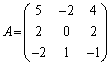 を対角化する。
を対角化する。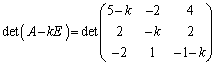
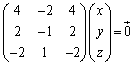
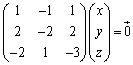
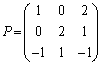 とすると、
とすると、