�ŗL�l�E�ŗL�x�N�g���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�t�s���A�s��ƘA��1�����������Q�Ƃ��Ă��������B
�����s��A�ɑ��āA�A���������F ���A
���A �ȊO�̉������Ƃ���k�̒l���A�s��A���ŗL�l�ƌ����B�܂��A����k�̒l�ɑ���
�ȊO�̉������Ƃ���k�̒l���A�s��A���ŗL�l�ƌ����B�܂��A����k�̒l�ɑ��� ���A�ŗL�lk�ɑ����ŗL�x�N�g���ƌ����B
���A�ŗL�lk�ɑ����ŗL�x�N�g���ƌ����B
�s��A�̌ŗL�lk�́A�������F �̉��Ƃ��ċ��߂���B���̕��������ŗL�������ƌ����B
�̉��Ƃ��ċ��߂���B���̕��������ŗL�������ƌ����B
 �́A�x�N�g��
�́A�x�N�g�� �ɍs��A�����������̂��A���Ƃ̃x�N�g���ƕ��s�ɂȂ�Ƃ������Ƃ��Ӗ����Ă��܂��B
�ɍs��A�����������̂��A���Ƃ̃x�N�g���ƕ��s�ɂȂ�Ƃ������Ƃ��Ӗ����Ă��܂��B
�E�ӂ��A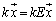 �Ƃ��č��ӂɈڍ�����ƁA
�Ƃ��č��ӂɈڍ�����ƁA

�����ŁA �����݂���Ƃ��āA�����炩����ƁA
�����݂���Ƃ��āA�����炩����ƁA

�� 
�ƂȂ�̂ŁA �͑��݂����A
�͑��݂����A
 �@(�t�s��(����3)���Q��)
�@(�t�s��(����3)���Q��)
A��n�������s�Ƃ��āA�ŗL���������A���������ď����ƁA
�ŗL�������́A �Ƃ��������܂ނ̂ŁAk�ɂ���n���������ɂȂ�܂��B
�Ƃ��������܂ނ̂ŁAk�ɂ���n���������ɂȂ�܂��B
�]���āAn���������̉��ł���An�������s��̌ŗL�l�́A�ő��n���邱�ƂɂȂ�܂��B
�ŗL�������ɂ����āA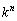 �Ƃ������́A
�Ƃ������́A �Ƃ��������炵���o�Ă��܂���B
�Ƃ��������炵���o�Ă��܂���B
�����W�J���āA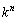 �̌W����1�ɂȂ�悤�ɏ����ƁA
�̌W����1�ɂȂ�悤�ɏ����ƁA
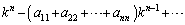
�Ƃ����`�ɂȂ�܂��B���̂Ƃ��ɏo�Ă���A�s��A�̑Ίp�����̘a�F ���s��A�̑Ίp�a�ƌ����A
���s��A�̑Ίp�a�ƌ����A �ƕ\���܂��B�܂��A�ŗL�������̒萔���́A
�ƕ\���܂��B�܂��A�ŗL�������̒萔���́A ��
��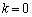 �Ƃ������́A�܂�A
�Ƃ������́A�܂�A �Ɉ�v���܂��B�]���āA�ŗL�������́A
�Ɉ�v���܂��B�]���āA�ŗL�������́A
 �@����@
�@����@
�Ƃ����`�����Ă��܂��B
��w�����œo�ꂷ��ŗL�������̂قƂ�ǂ�2���̐����s�� �Ɋւ�����̂ł��B
�Ɋւ�����̂ł��B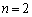 �̏ꍇ�A�ŗL�������́A
�̏ꍇ�A�ŗL�������́A
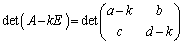
�@
�@
�ƂȂ�A�@�̌`�����Ă��܂��B
��D �̂Ƃ��A
�̂Ƃ��A (
(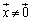 )��������k (�ŗL�l)�ƃx�N�g��
)��������k (�ŗL�l)�ƃx�N�g��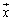 (�ŗL�x�N�g��)�����߂�B
(�ŗL�x�N�g��)�����߂�B
[��]�@
�@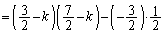
�@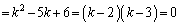
��  ......[��]
......[��]
�s��A�̌ŗL�l��2��3�ł��B
 �̂Ƃ��A
�̂Ƃ��A
�� 
�Ⴆ�A �C
�C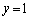
�ŗL�l2�ɑΉ�����ŗL�x�N�g���́At�������Ƃ��āA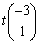
 �̂Ƃ��A
�̂Ƃ��A
�� 
�Ⴆ�A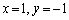
�ŗL�l3�ɑΉ�����ŗL�x�N�g���́As�������Ƃ��āA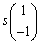
���߂�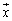 �́A
�́A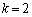 �̂Ƃ��A
�̂Ƃ��A �C
�C �̂Ƃ��A
�̂Ƃ��A ......[��]
......[��]
�s��A�ɂ́A�ŗL�̕������A �̕�����
�̕�����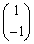 �̕�����2�����āA
�̕�����2�����āA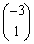 �ƕ��s�ȃx�N�g����A���������2�{����A
�ƕ��s�ȃx�N�g����A���������2�{����A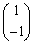 �ƕ��s�ȃx�N�g����A���������3�{�����A�Ƃ������Ƃ������Ă��܂��B
�ƕ��s�ȃx�N�g����A���������3�{�����A�Ƃ������Ƃ������Ă��܂��B
�Ȃ��An�������s��A�̈قȂ�ŗL�l�ɑ���ŗL�x�N�g�� �C
�C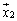 �C�����1���Ɨ��ł��B�Ȃ��Ȃ�A����i�Cj (
�C�����1���Ɨ��ł��B�Ȃ��Ȃ�A����i�Cj ( �C
�C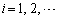 �C
�C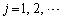 )���Ƃ�A�قȂ�ŗL�l
)���Ƃ�A�قȂ�ŗL�l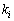 �C
�C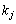 �ɑ���ŗL�x�N�g��
�ɑ���ŗL�x�N�g��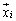 �C
�C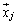 �ɂ��āA
�ɂ��āA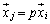 (p�͎���)�Ə������Ƃ���ƁA
(p�͎���)�Ə������Ƃ���ƁA ���A
���A
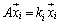 �C
�C
�Ƃ���2�ʂ�̎��������Ă��܂��A�ӁX�����ƁA
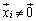 ���A
���A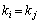 �ƂȂ��āA�قȂ�ŗL�l
�ƂȂ��āA�قȂ�ŗL�l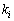 �C
�C �Ƃ�������Ɩ������邩��ł��B
�Ƃ�������Ɩ������邩��ł��B
�]���āAn�������s��A�̈قȂ�ŗL�l�ɑ���n�̌ŗL�x�N�g��(���A���݂����Ƃ���)����ׂč�����s��F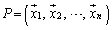 �Ƃ����`�̍s������ƁAP�͐���(�t�s��
�Ƃ����`�̍s������ƁAP�͐���(�t�s��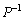 �����݂���)�ł��B�Ȃ��Ȃ�A�ŗL�x�N�g���͗�x�N�g���łȂ��A�s�̐������A
�����݂���)�ł��B�Ȃ��Ȃ�A�ŗL�x�N�g���͗�x�N�g���łȂ��A�s�̐������A (p�͎���)�Ə����Ȃ���A
(p�͎���)�Ə����Ȃ���A ������ł��B
������ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
 �̂Ƃ��A
�̂Ƃ��A

