�s��ƘA��1���������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�s���A�s��̐��A�t�s�����Q�Ƃ��Ă��������B
�A��1���������F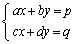
���s��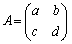 �C
�C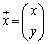 �C
�C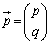 ��p���ĕ\���ƁA
��p���ĕ\���ƁA
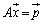
���̍s��A��A���������̌W���s��ƌ����܂��B
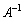 �����݂���Ƃ��A�܂�A
�����݂���Ƃ��A�܂�A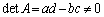 �ł���Ƃ��A���́A
�ł���Ƃ��A���́A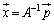
2���A��1�����������l���܂��B��L�̂悤�ɍs���p���āA
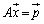
�ƕ\����Ă���Ƃ��A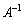 �����݂���Ȃ�A���ӂɍ�����
�����݂���Ȃ�A���ӂɍ�����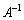 �������āA
�������āA
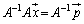
�� 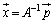
����ŁA�A���������̉������߂��܂��B
��1�D�@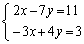
�s���p���āA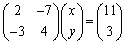
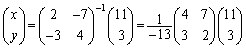
�@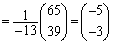
�� 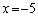 �C
�C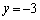 ......[��]
......[��]
2���A��1���������̏ꍇ�A�s���p��������A���ʂ�1�����������ċ��߂�������������m��܂��A100���A��1���������A1�����A��1���������Ƃ��������������v�Z�@�ʼn������邱�Ƃ܂ōl����ƁA2���A��1�����������s��ň������Ƃɂ��L�p�Ȓm����������̂ł��B
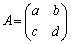 �C
�C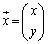 �C
�C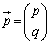 �Ƃ��āA
�Ƃ��āA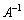 �����݂��Ȃ��Ƃ��A�܂�A
�����݂��Ȃ��Ƃ��A�܂�A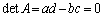 �̂Ƃ��ɂ��čl���Ă݂܂��B
�̂Ƃ��ɂ��čl���Ă݂܂��B
�A���A�������Ƃ��ĈӖ������悤�ɁAa�Cb�͓�����0�ł͂Ȃ��Ac�Cd�͓�����0�ł͂Ȃ����Ƃɂ��܂��B
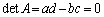 �̂Ƃ��A
�̂Ƃ��A
(i) 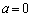 ���Ƃ���ƁA
���Ƃ���ƁA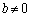 �Ȃ̂ŁA
�Ȃ̂ŁA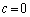 �C�܂��A
�C�܂��A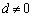 �ł��B
�ł��B
���̂Ƃ��́A�A���������́A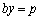 �C
�C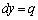 �ƂȂ�A
�ƂȂ�A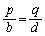 �̂Ƃ��ɂ́A����
�̂Ƃ��ɂ́A����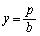 ��̂��ׂĂ̓_�̍��W�����ƂȂ�A
��̂��ׂĂ̓_�̍��W�����ƂȂ�A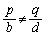 �̂Ƃ��ɂ͉��͑��݂��܂���B
�̂Ƃ��ɂ͉��͑��݂��܂���B
(ii) 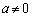 �̂Ƃ��A
�̂Ƃ��A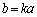 �Ƃ����ƁA
�Ƃ����ƁA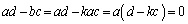
�� 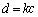
���̂Ƃ��́A�A���������́A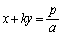 �C
�C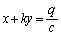 �ƂȂ�A
�ƂȂ�A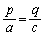 �̂Ƃ��ɂ́A����
�̂Ƃ��ɂ́A����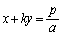 ��̂��ׂĂ̓_�̍��W�����ƂȂ�A
��̂��ׂĂ̓_�̍��W�����ƂȂ�A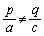 �̂Ƃ��ɂ͉��͑��݂��܂���B
�̂Ƃ��ɂ͉��͑��݂��܂���B
�ȏ�ŁA(i)��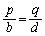 �̂Ƃ��A(ii)��
�̂Ƃ��A(ii)��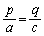 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A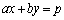 �C
�C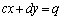 �͓���̒�����\���Ă���A������̓_�̍��W�͂��ׂĉ��ƂȂ�܂��B���̂Ƃ��ɂ́A�A���������̉��͖����ɂ��邱�ƂɂȂ�A�A���������́u�s��v�ł���ƌ����܂��B
�͓���̒�����\���Ă���A������̓_�̍��W�͂��ׂĉ��ƂȂ�܂��B���̂Ƃ��ɂ́A�A���������̉��͖����ɂ��邱�ƂɂȂ�A�A���������́u�s��v�ł���ƌ����܂��B
(i)��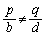 �̂Ƃ��A(ii)��
�̂Ƃ��A(ii)��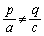 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A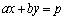 �C
�C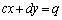 �́A�قȂ镽�s2������\���Ă���A���s2�����͌�_�������Ȃ��̂ŁA�A���������̉��͑��݂��܂���B���̂Ƃ��ɂ́A�A���������́u�s�\�v�ł���ƌ����܂��B
�́A�قȂ镽�s2������\���Ă���A���s2�����͌�_�������Ȃ��̂ŁA�A���������̉��͑��݂��܂���B���̂Ƃ��ɂ́A�A���������́u�s�\�v�ł���ƌ����܂��B
��2�D�A���������F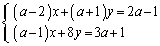 �̉����A����a�̒l�ɂ���Ăǂ̂悤�ɕς�邩�ׂ�B
�̉����A����a�̒l�ɂ���Ăǂ̂悤�ɕς�邩�ׂ�B
[��]�@�W���s��́A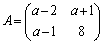
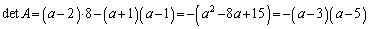
����āA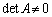 �C�����A
�C�����A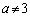 ����
���� 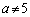 �̂Ƃ��ɂ́A����1�g�̉������B
�̂Ƃ��ɂ́A����1�g�̉������B
 �̂Ƃ��ɂ́A�A���������́A�Ƃ��ɁA
�̂Ƃ��ɂ́A�A���������́A�Ƃ��ɁA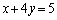 �ƂȂ�A�����F
�ƂȂ�A�����F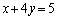 ��̂��ׂĂ̓_�̍��W�����ƂȂ�A���͖����ɂ���B
��̂��ׂĂ̓_�̍��W�����ƂȂ�A���͖����ɂ���B
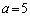 �̂Ƃ��ɂ́A�A���������́A
�̂Ƃ��ɂ́A�A���������́A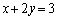 �C
�C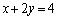 �ƂȂ�A�قȂ镽�s2������\���̂ŁA���͑��݂��Ȃ��B
�ƂȂ�A�قȂ镽�s2������\���̂ŁA���͑��݂��Ȃ��B
��3�D�A���������F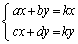 ���A
���A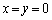 �ȊO�ɂ��������悤��k�̒l���߂�B
�ȊO�ɂ��������悤��k�̒l���߂�B
[��]�@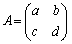 �C
�C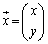 �Ƃ���ƁA�A���������́A
�Ƃ���ƁA�A���������́A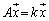 �@����@�@�Ə����܂��B
�@����@�@�Ə����܂��B
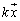 �����ӂɈڍ����āA
�����ӂɈڍ����āA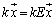 (E��2���̒P�ʍs��)�ƌ���ƁA
(E��2���̒P�ʍs��)�ƌ���ƁA
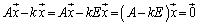 �@����A
�@����A
�����ŁA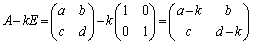 ���t�s��
���t�s��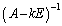 �����Ƃ���ƁA�A�̍����炩���āA
�����Ƃ���ƁA�A�̍����炩���āA
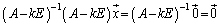
�� 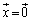
����ł́A�A���������̉����A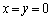 �����ɂȂ��Ă��܂��܂��B�]���āA
�����ɂȂ��Ă��܂��܂��B�]���āA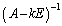 �͑��݂��܂���B�܂�A
�͑��݂��܂���B�܂�A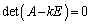 �ł��B
�ł��B
�� 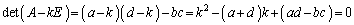
�� 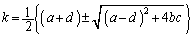 ......[��]
......[��]
3���ȏ�̘A��1���������ɂ��ẮA��{�ό`���Q�Ƃ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B