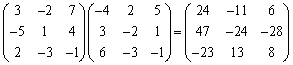行列の積 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目では、行列も参照してください。
2個のベクトル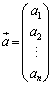 ,
,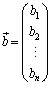 の積:
の積:
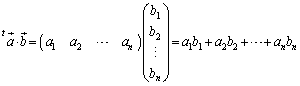 (左側を行ベクトル、右側を列ベクトルにする。数学Bに出てくるベクトルの内積だと思えばよい)
(左側を行ベクトル、右側を列ベクトルにする。数学Bに出てくるベクトルの内積だと思えばよい)
m×l行列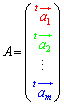 ,l×n行列
,l×n行列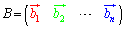 として、
として、
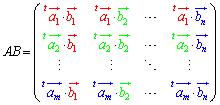 (m×l行列とl×n行列の積はm×n行列)
(m×l行列とl×n行列の積はm×n行列)
ただし、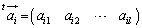 ,
,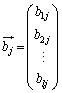 (
(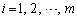 ,
,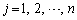 )
)
特に、2次の正方行列どうしの積は、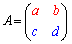 ,
,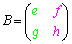 として、
として、

行列の積ABにおいては、左側Aの列数と右側Bの行数が同じでないと積の計算が行えないことに注意してください。
行列の積ABの行数は、左側Aの行数に一致し、列数は右側Bの列数に一致します。
2次の正方行列どうしの積については、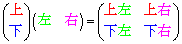 というように覚えましょう。
というように覚えましょう。
3次の正方行列どうしの積については、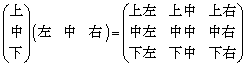 となっています。
となっています。
左側の行列を横に見て、上中下と分け、右側の行列を縦に見て、左中右と分ける。各組合わせごとに内積を計算します。
行列の積では、左側にくるものと右側にくるものとで扱いが違うので、積の左右を入れ替えると、一般に異なる行列になります。
つまり、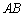 と
と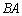 が異なるのがふつうです。
が異なるのがふつうです。
従って、行列の計算では、一般に、
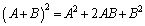 ,
,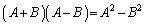
のように計算することができません。こうなるのは、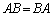 のときだけです。正しくは、
のときだけです。正しくは、
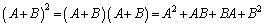
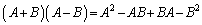
従って、3つのn次正方行列A,B,Cがあり、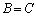 というような等式があって行列Aをかける場合、左からかけるのか、右からかけるのかを明記する必要があります。
というような等式があって行列Aをかける場合、左からかけるのか、右からかけるのかを明記する必要があります。
左からかけると、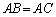 となり、
となり、
右からかけると、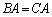 となります。
となります。
左からかけるのと、右からかけるのとでは、通常違う結果となるので注意してください。
例1. 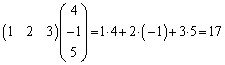 (数学Bの内積:
(数学Bの内積: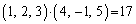 と同じです)
と同じです)
例2.(1) 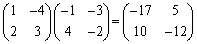 ,
,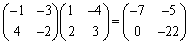 (左右を入れ替えると積が異なる)
(左右を入れ替えると積が異なる)
(2) 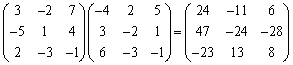
行列の積について、以下のことが成り立ちます。
(1) 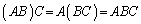
(2) 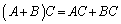 ,
,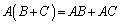
一般的に証明すると大がかりなので、A,B,Cが2次正方行列の場合で確かめておきます。
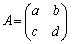 ,
,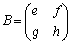 ,
,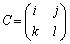 として、
として、
(1) 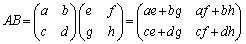
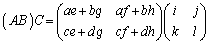
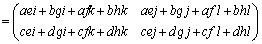
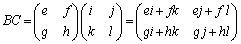
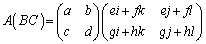
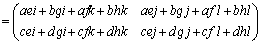
∴ 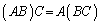 (この積を単に
(この積を単に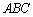 とも書きます)
とも書きます)
(2) 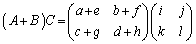
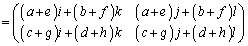
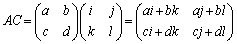
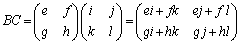
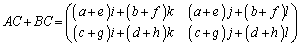
∴ 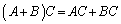
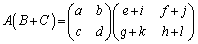
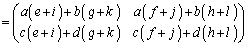
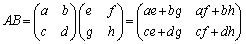
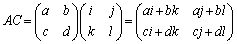
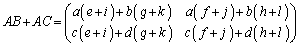
∴ 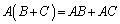
また、実数倍と行列の積については、入れ替えて計算することができます。つまり、
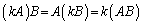
これも、2次正方行列の場合で確かめておきます。
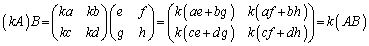
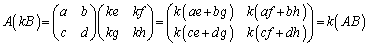
∴ 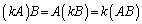 (この積を単に
(この積を単に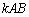 と書きます)
と書きます)
n次正方行列A,n次単位行列E、n次正方行列の零行列Oとの積について以下のことが成り立ちます。
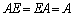 ,
,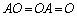
わかりづらくなりますが、行列の積を成分に着目して、以下のように見ることもできます。
I行J列の行列A,J行M列の行列B,M行N列の行列Cの積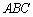 を考えてみます。
を考えてみます。
行列Aの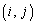 成分を
成分を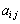 (
(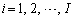 ,
,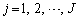 )
)
行列Bの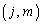 成分を
成分を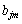 (
(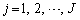 ,
,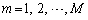 )
)
行列Cの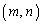 成分を
成分を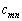 (
(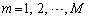 ,
,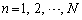 )
)
とします。
行列の積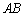 の
の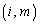 成分は、
成分は、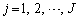 について行列Aの
について行列Aの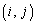 成分と行列Bの
成分と行列Bの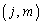 成分をかけて足し合わせたもので、
成分をかけて足し合わせたもので、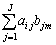 となります。
となります。
行列の積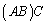 の
の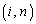 成分は、
成分は、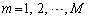 について行列
について行列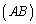 の
の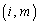 成分と行列Cの
成分と行列Cの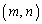 成分をかけて足し合わせたもので、
成分をかけて足し合わせたもので、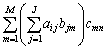 となります。
となります。
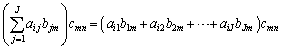
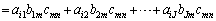
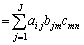
よって、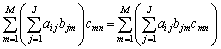
同様に、行列の積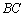 の
の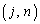 成分は、
成分は、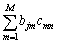
行列の積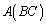 の
の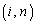 成分は、
成分は、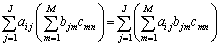
Σ記号の順番は入れ替えても和の値には影響ありません。長方形に並んだ数を横に足してから縦に足すか、縦に足してから横に足すか、という違いだけです。
よって、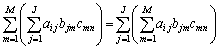
これで、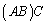 と
と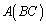 のすべての成分について等しいことが言えるので、
のすべての成分について等しいことが言えるので、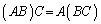 です。
です。
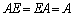 については、フーリエ級数のところで出てくる、クロネッカーのデルタ記号:
については、フーリエ級数のところで出てくる、クロネッカーのデルタ記号: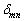 の利用が便利です。
の利用が便利です。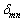 は、
は、
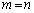 のときに、
のときに、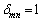 ,
,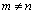 のときに、
のときに、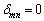
と定義されるので、単位行列の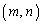 成分そのものです。
成分そのものです。
n次正方行列Aの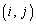 成分を
成分を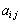 (
(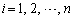 ,
,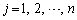 ),n次単位行列の
),n次単位行列の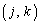 成分をクロネッカーのデルタ記号を利用して
成分をクロネッカーのデルタ記号を利用して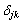 とすると、
とすると、
積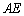 の
の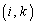 成分は、
成分は、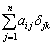
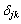 は、
は、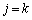 のときのみ1で残りは0なので、和は、
のときのみ1で残りは0なので、和は、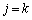 のところだけが生き残って、
のところだけが生き残って、
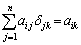
つまり、積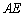 の
の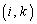 成分は
成分は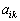 です。ということは、
です。ということは、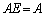 ということです。
ということです。
同様に、積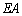 の
の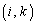 成分は、
成分は、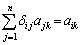
よって、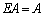
これで、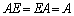
が言えます。
目がチカチカしますが、将来、相対性理論をやろうという意欲をお持ちの方は、「縮約」というのですが、こういう計算が腐るほど出てくるので、よく慣れておいてください。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 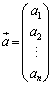 ,
,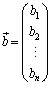 の積:
の積: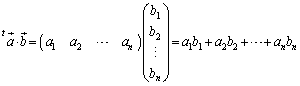
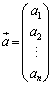 ,
,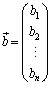 の積:
の積: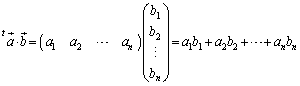 (左側を行ベクトル、右側を列ベクトルにする。数学Bに出てくるベクトルの内積だと思えばよい)
(左側を行ベクトル、右側を列ベクトルにする。数学Bに出てくるベクトルの内積だと思えばよい) ,l×n行列
,l×n行列 (m×l行列とl×n行列の積はm×n行列)
(m×l行列とl×n行列の積はm×n行列)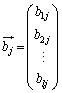 (
(
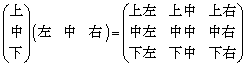 となっています。
となっています。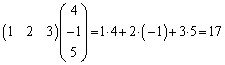 (数学Bの内積:
(数学Bの内積: