�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
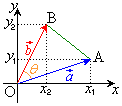 (1) �E�}�̂悤�ɁA2���x�N�g��
(1) �E�}�̂悤�ɁA2���x�N�g��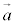 �C
�C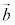 �̂Ȃ��p��θ �̂Ƃ��A
�̂Ȃ��p��θ �̂Ƃ��A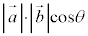 ��
��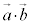 �Ə����������ƌ����B
�Ə����������ƌ����B
�@�����A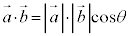
(2) 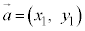 �C
�C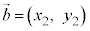 �̂Ƃ��A
�̂Ƃ��A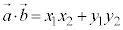 �@(�x�N�g���̐����\�����Q��)
�@(�x�N�g���̐����\�����Q��)
(3) 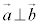 �̂Ƃ��A
�̂Ƃ��A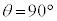 ��
��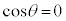 �ƂȂ�A
�ƂȂ�A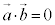
�@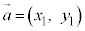 �C
�C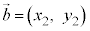 �ł����āA
�ł����āA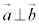 �̂Ƃ��A
�̂Ƃ��A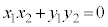
(4) 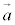 �C
�C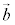 ����������������Ă��āA
����������������Ă��āA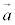 �C
�C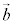 �̂Ȃ��p��0�̂Ƃ�
�̂Ȃ��p��0�̂Ƃ�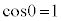 ���A
���A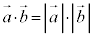
�@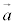 �C
�C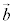 �������̕����������Ă��āA
�������̕����������Ă��āA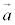 �C
�C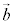 �̂Ȃ��p��
�̂Ȃ��p��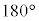 �̂Ƃ�
�̂Ƃ�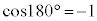 ���A
���A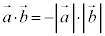
�@���ɁA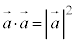
(1) 2�̃x�N�g���̂Ȃ��pθ �́A�ʏ�́A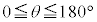 �ƂȂ�悤�ɂƂ�܂��B
�ƂȂ�悤�ɂƂ�܂��B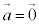 �܂���
�܂���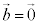 �̂Ƃ��́A�Ȃ��p�𑪂邱�Ƃ��ł��܂��A
�̂Ƃ��́A�Ȃ��p�𑪂邱�Ƃ��ł��܂��A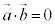 �Ƃ��܂��B
�Ƃ��܂��B
(4)�ŁA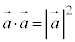 ���A
���A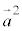 �Ə����Ȃ��悤�ɂ��Ă��������B�x�N�g���ɂ͓��ς̑��ɁA�u�O�ρv�ƌĂ��ς������āA���ςƂ��Ă�2��Ȃ̂��A�O�ςƂ��Ă�2��Ȃ̂�����ʂ��邱�Ƃ��ł��܂���B���ςƂ��Ă�2��́A�ʓ|�ł��A
�Ə����Ȃ��悤�ɂ��Ă��������B�x�N�g���ɂ͓��ς̑��ɁA�u�O�ρv�ƌĂ��ς������āA���ςƂ��Ă�2��Ȃ̂��A�O�ςƂ��Ă�2��Ȃ̂�����ʂ��邱�Ƃ��ł��܂���B���ςƂ��Ă�2��́A�ʓ|�ł��A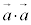 �Ə����悤�ɂ��܂��傤�B
�Ə����悤�ɂ��܂��傤�B
(2)�̏ؖ��@�E��}�ŁA�_A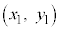 �C�_B
�C�_B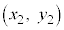 �C
�C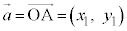 �C
�C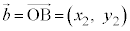 �C
�C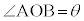 �Ƃ��āA
�Ƃ��āA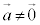 �C
�C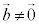 �C
�C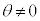 �C
�C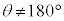 �Ƃ��܂��B
�Ƃ��܂��B
�]���藝���A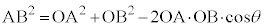 �@����@
�@����@
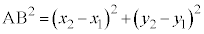
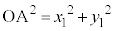 �C
�C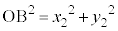 �C
�C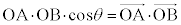
�������@�ɑ������ƁA
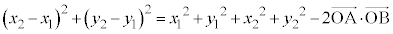
���ӂ�W�J���Đ��������
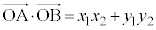
�������܂��B
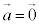 �܂���
�܂���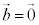 �̂Ƃ��́A
�̂Ƃ��́A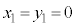 �܂���
�܂���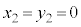 �ł����āA������ɂ��Ă��A
�ł����āA������ɂ��Ă��A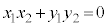 �ł��B
�ł��B
����āA(2)���������܂��B
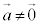 �C
�C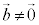 �ł����āA
�ł����āA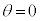 �܂���
�܂���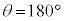 �̂Ƃ��́A
�̂Ƃ��́A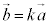 �C�܂�A
�C�܂�A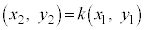 �Ƃ������Ƃ��ł��āA
�Ƃ������Ƃ��ł��āA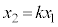 �C
�C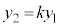 �ƂȂ�܂��B
�ƂȂ�܂��B
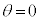 �̂Ƃ��A
�̂Ƃ��A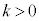 �C(1)�ɂ��ƁA
�C(1)�ɂ��ƁA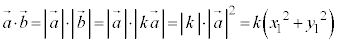
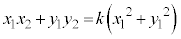
����āA(2)���������܂��B
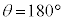 �̂Ƃ��A
�̂Ƃ��A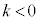 �C(1)�ɂ��ƁA
�C(1)�ɂ��ƁA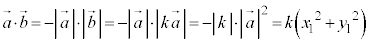
����āA(2)���������܂��B
(�ؖ��I)
��1�D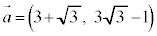 �C
�C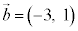 �̂Ƃ��A
�̂Ƃ��A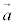 ��
��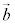 �̂Ȃ��pθ (
�̂Ȃ��pθ (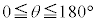 )�����߂�B
)�����߂�B
[��]�@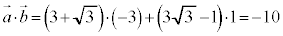
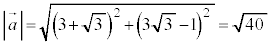
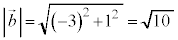
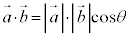 ���A
���A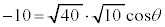
�� 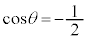
�� 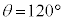 ......[��]
......[��]
��2�D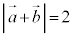 �C
�C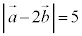 �C
�C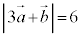 �̂Ƃ��A
�̂Ƃ��A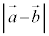 �����߂�B
�����߂�B
[��]�@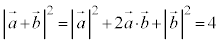 �@����@
�@����@
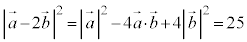 �@����A
�@����A
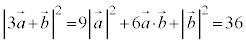 �@����B
�@����B
�A�|�@���A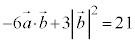
�� 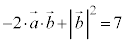 �@����C
�@����C
�@�~9�|�B���A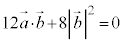
�� 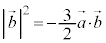
�C�ɑ�����āA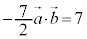
�� 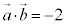 �C
�C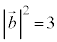
�@���A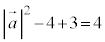
�� 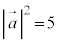
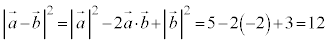
�� 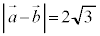 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B