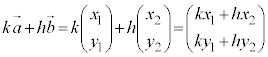ベクトルの成分表示 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目については、ベクトルとは、および、ベクトルの1次独立を参照してください。
(1) 大きさが1のベクトルを基本ベクトルと言う。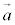
が基本ベクトルのとき、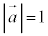
(2) 右図1のように、座標平面上で点
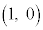の位置ベクトル(原点を始点とするベクトル)を
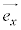，点
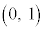の位置ベクトルを
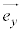とすると、
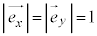より、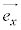
，
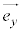は基本ベクトルである(また、1次独立である)。座標平面上の任意の点P
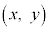の位置ベクトル
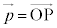を、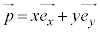
と表すことができる。
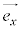の係数xを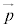
のx成分，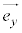
の係数を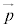
のy成分と言う。
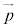のx成分は点Pのx座標であり、
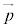のy成分は点Pのy座標である。
そこで、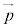
を点Pの座標と同じようにして、
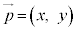と表すことにする。これを、
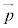の成分表示と言う。
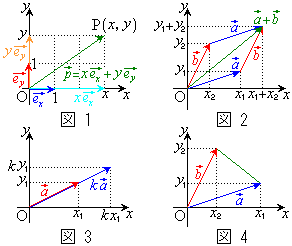
(3) 
，
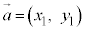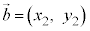と成分表示されているとき、右図2のように、
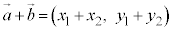となる。成分表示でベクトルの和を考えるときは、x成分同士の和をx成分、y成分同士の和をy成分とすればよい(ベクトルの差も同様)。
(4) 
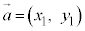と成分表示されているとき、右図3のように、
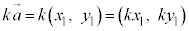となる。成分表示でベクトルの実数倍を考えるときは、x成分、y成分のそれぞれに実数をかければよい。
(5) 
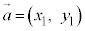と成分表示されているとき、右図4のように、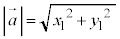
(6) 右図4のように、座標平面上で点A，点Bの位置ベクトルを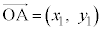
，
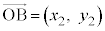とするとき、
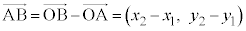より、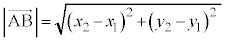
(2) 基本ベクトルは座標系を決めているという言い方もできます。2つの基本ベクトル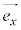
，
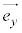が互いに垂直になっているときに、
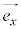がx軸の向きとx軸の目盛りの1を決め、
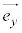がy軸の向きとy軸の目盛りの1を決めているのです。こうした座標系を正規直交座標系と呼びます。
(3)，(4)をまとめると、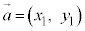
，
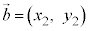と成分表示されているとき、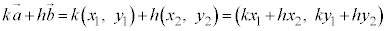
(x同士かけて足す、y同士かけて足す)
実際の計算を行うときには、以下のようにベクトルを縦に書いて、上同士、下同士で計算し、見間違いのないように注意してください。
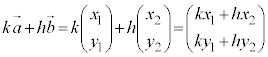
(5)，(6)については、2点間の距離について、座標平面を参照してください。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。