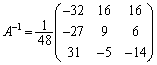基本変形
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、行列、行列の積、逆行列を参照してください。なお、基本変形は、大学入試ではほとんど出題されないテーマです。どうしても、3次以上の行列の逆行列の求め方が知りたい、という人のための項目です。
連立方程式: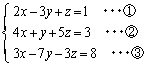
を解くことを考えます。①~③を行列を用いて書くと、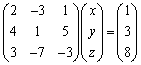 ・・・④
・・・④
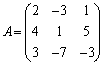 ,
,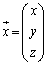 ,
,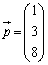 として、
として、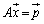 ・・・⑤
・・・⑤
まず、zを消去します。
①×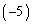 +②より、
+②より、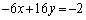 ・・・⑥
・・・⑥
これが、行列を用いて書かれた連立方程式④では、どういうことになっているかを考えてみます。
②の代わりに、⑥を考えても方程式を解くことができるので、④の行列Aの第2行を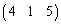 から
から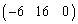 に入れ替えた行列
に入れ替えた行列
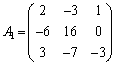
を考え、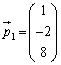 として、
として、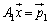 を解けばよい、ということを意味しています。
を解けばよい、ということを意味しています。
Aから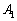 を作る方法を考えてみます。Aの第1行と第3行には影響を与えず、第2行については、Aの第1行の
を作る方法を考えてみます。Aの第1行と第3行には影響を与えず、第2行については、Aの第1行の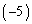 倍をAの第2行に加え合わせたものが来るようにすればよいので、
倍をAの第2行に加え合わせたものが来るようにすればよいので、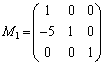 という行列を考え、これをAの左からかけてやると、
という行列を考え、これをAの左からかけてやると、
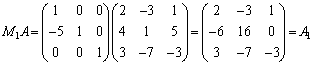
つまり、連立方程式の②を⑥に置き換えたい場合には、行列の第2行のところを、①にかける数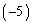 を
を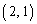 成分、②にかける数1を
成分、②にかける数1を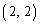 成分、③にかける数0を
成分、③にかける数0を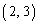 成分とし、行列の第1行は①そのままにするのであれば
成分とし、行列の第1行は①そのままにするのであれば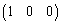 ,行列の第3行は③そのままにするのであれば
,行列の第3行は③そのままにするのであれば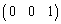 としたものを
としたものを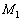 として、もとの行列Aにかけてやればよいのです。④右辺についても、
として、もとの行列Aにかけてやればよいのです。④右辺についても、
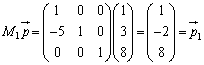
次に、①×3+③より、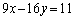 ・・・⑦
・・・⑦
③を⑦に入れ替えても方程式を解くことができるので、行列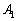 の第3行を
の第3行を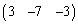 から
から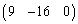 に入れ替えた行列
に入れ替えた行列
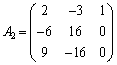
を考え、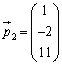 として、
として、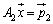 を解けばよい、ということになります。
を解けばよい、ということになります。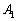 から
から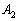 を作る行列は、先ほどと同じように考えて、第1行は
を作る行列は、先ほどと同じように考えて、第1行は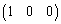 ,第2行は
,第2行は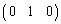 ,第3行は
,第3行は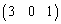 とした行列を
とした行列を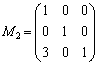 とすれば、
とすれば、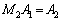 となります。右辺についても、
となります。右辺についても、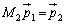
次に、⑥+⑦より、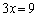
両辺を3で割って、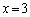 ・・・⑧
・・・⑧
となるのですが、これは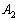 の第1行と第2行を変えないで、第3行に第2行を加えたものが入るので、
の第1行と第2行を変えないで、第3行に第2行を加えたものが入るので、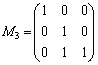 ,
,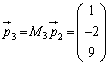 として、
として、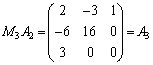 ,
,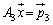
さらに、第1行と第2行を変えないで、第3行を3で割るので、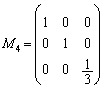 ,
,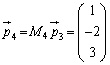 として、
として、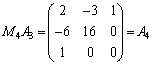 ,
,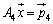
次にyを求めるために、⑥に⑧の6倍を加えると、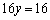 ,両辺を16で割って、
,両辺を16で割って、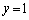 ・・・⑨
・・・⑨
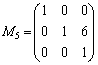 ,
,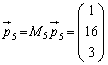 ,
,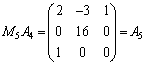 ,
,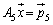
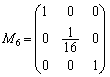 ,
,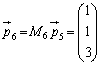 ,
,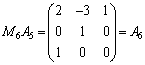 ,
,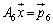
最後に、①に⑧の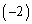 倍を加えると、
倍を加えると、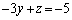
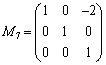 ,
, ,
,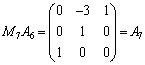 ,
,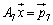
さらに、⑨の3倍を加えて、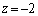
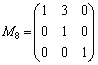 ,
,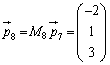 ,
,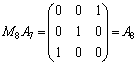 ,
,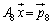
これで解が求まっているのですが、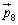 に上からzの解、yの解、xの解、と並んでしまうので、第2行を変えないで、第1行と第3行を入れ替えることにします。このためには、
に上からzの解、yの解、xの解、と並んでしまうので、第2行を変えないで、第1行と第3行を入れ替えることにします。このためには、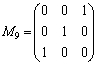 という行列を
という行列を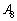 に左からかけます。
に左からかけます。
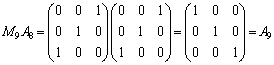 (
(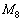 が第3行を第1行に移し、第1行を第3行に移しているのをよく理解してください)
が第3行を第1行に移し、第1行を第3行に移しているのをよく理解してください)
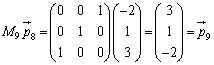
これで、最終形は、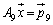 ,即ち、
,即ち、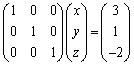 となるので、きれいに、
となるので、きれいに、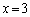 ,
,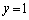 ,
,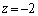 という解の形が出てきます。
という解の形が出てきます。
さて、以上の過程で何をしたのかと言うと、元々の方程式⑤の両辺に、左から、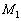 ,
,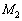 ,・・・,
,・・・,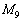 を順次かけて、最終的に、
を順次かけて、最終的に、
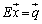 (Eは単位行列)
(Eは単位行列)
という形を作ったのです。このときの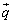 が連立方程式の解になっているのです。
が連立方程式の解になっているのです。
つまり、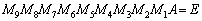 となるようにすれば、
となるようにすれば、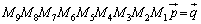 が連立方程式の解になる、ということです。
が連立方程式の解になる、ということです。
また、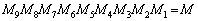 は、Aの逆行列になっています。
は、Aの逆行列になっています。
3次以上の正方行列の逆行列は、この方法によって求めるのがラクです。コンピュータのプログラミングにも向いた方法です。
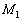 ~
~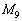 は3つのタイプに分類できます。
は3つのタイプに分類できます。
(i) 第i行に第j行のk倍を加える。上記の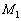 ,
,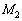 ,
,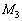 ,
,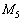 ,
,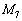 ,
,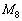 がこのタイプです。
がこのタイプです。
(ii) 第i行をk倍する。上記の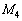 ,
,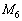 がこのタイプです。
がこのタイプです。
(iii) 第i行と第j行を入れ替える。上記の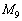 がこのタイプです。
がこのタイプです。
以上の操作では、この3種類の変形を行うことにより、正方行列Aの逆行列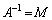 を求めていたのです。
を求めていたのです。
正方行列が逆行列を持てば、この方法で必ず逆行列が求められることが証明されています。
この3種類の変形は(左)基本変形と呼ばれています。
実際に、逆行列を求める場合には、行列Aの右に単位行列Eをつけた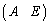 という形の行列に基本変形を施し、最終的に
という形の行列に基本変形を施し、最終的に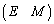 という形が得られるとすると、このMが
という形が得られるとすると、このMが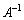 になります。
になります。
上記の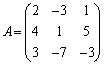 では、以下のようになります。右の方から順々に行列の成分を0にしていくように変形するのがコツです。
では、以下のようになります。右の方から順々に行列の成分を0にしていくように変形するのがコツです。
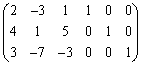
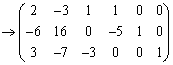 (第2行に第1行の
(第2行に第1行の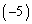 倍を加えた)
倍を加えた)
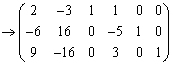 (第3行に第1行の3倍を加えた)
(第3行に第1行の3倍を加えた)
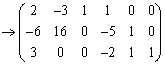 (第3行に第2行を加えた)
(第3行に第2行を加えた)
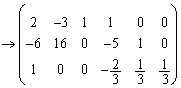 (第3行に
(第3行に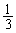 をかけた)
をかけた)
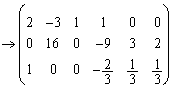 (第2行に第3行の6倍を加えた)
(第2行に第3行の6倍を加えた)
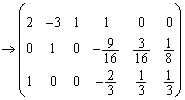 (第2行を16で割った)
(第2行を16で割った)
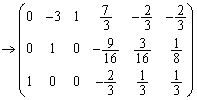 (第1行に第3行の
(第1行に第3行の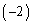 倍を加えた)
倍を加えた)
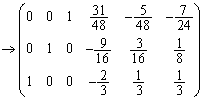 (第1行に第2行の3倍を加えた)
(第1行に第2行の3倍を加えた)
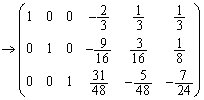 (第1行と第3行を入れ替えた)
(第1行と第3行を入れ替えた)
よって、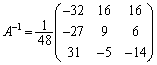
なお、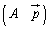 に上記と同じような操作を行い、最終的に
に上記と同じような操作を行い、最終的に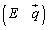 という形になれば、この
という形になれば、この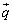 が連立方程式
が連立方程式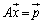 の解を与えます。
の解を与えます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
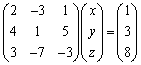 ・・・④
・・・④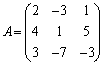 ,
,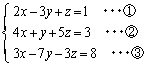
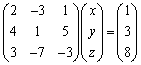 ・・・④
・・・④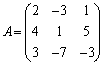 ,
,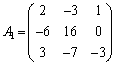
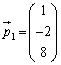 として、
として、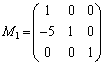 という行列を考え、これをAの左からかけてやると、
という行列を考え、これをAの左からかけてやると、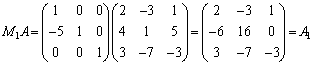
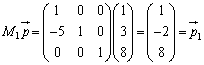
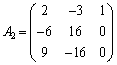
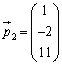 として、
として、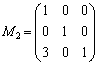 とすれば、
とすれば、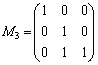 ,
,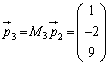 として、
として、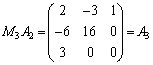 ,
,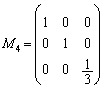 ,
,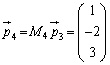 として、
として、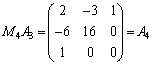 ,
,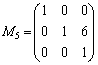 ,
,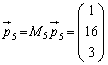 ,
,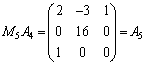 ,
,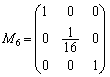 ,
,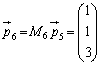 ,
,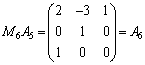 ,
,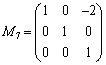 ,
, ,
,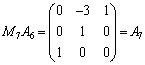 ,
,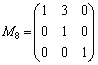 ,
,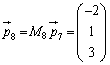 ,
,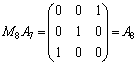 ,
,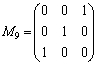 という行列を
という行列を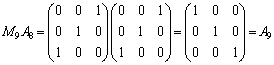 (
(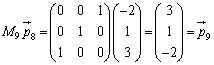
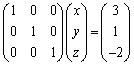 となるので、きれいに、
となるので、きれいに、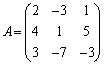 では、以下のようになります。右の方から順々に行列の成分を0にしていくように変形するのがコツです。
では、以下のようになります。右の方から順々に行列の成分を0にしていくように変形するのがコツです。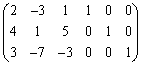
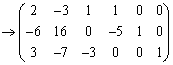 (第2行に第1行の
(第2行に第1行の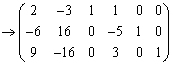 (第3行に第1行の3倍を加えた)
(第3行に第1行の3倍を加えた)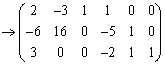 (第3行に第2行を加えた)
(第3行に第2行を加えた)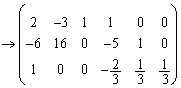 (第3行に
(第3行に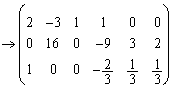 (第2行に第3行の6倍を加えた)
(第2行に第3行の6倍を加えた)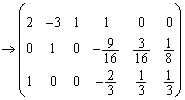 (第2行を16で割った)
(第2行を16で割った)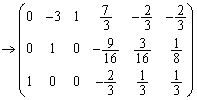 (第1行に第3行の
(第1行に第3行の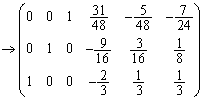 (第1行に第2行の3倍を加えた)
(第1行に第2行の3倍を加えた)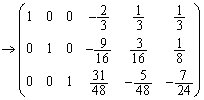 (第1行と第3行を入れ替えた)
(第1行と第3行を入れ替えた)