逆行列 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目では、行列、行列の積を参照してください。
正方行列Aに対して、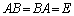 (E:単位行列)をみたす行列Bを、Aの逆行列と言い、
(E:単位行列)をみたす行列Bを、Aの逆行列と言い、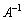 (A-inverseと読みます)と書く。
(A-inverseと読みます)と書く。
即ち、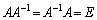
2次の正方行列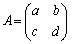 に対し、
に対し、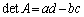 をAの行列式と言う。行列式は、
をAの行列式と言う。行列式は、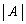 ,
,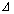 のようにも表す。
のようにも表す。
Aは、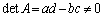 のときに、逆行列
のときに、逆行列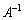 をもち、
をもち、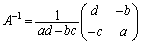 (*)
(*)
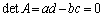 のときには、行列Aは、逆行列
のときには、行列Aは、逆行列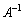 をもたない。
をもたない。
正方行列Aが逆行列をもつときは、1つしか逆行列をもちません。仮に、Aの逆行列がB,Cの2つあったとする(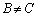 )と、
)と、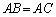 (
(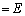 )ですが、左から
)ですが、左から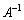 をかけると、
をかけると、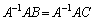
∴ 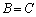
となって矛盾を生じます。
(*)は、行列の積を計算してみると、
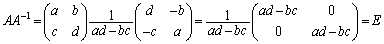
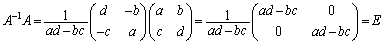
よって、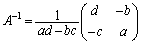 です。
です。
n次(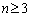 )の正方行列の場合の行列式の公式は複雑です。少なくとも大学入試では不要です。
)の正方行列の場合の行列式の公式は複雑です。少なくとも大学入試では不要です。
注.実は、クラメールの公式と呼ばれる公式があるのですが、基本変形による方が遙かに簡単です。
行列Aが逆行列をもつ、つまり、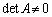 のとき、行列Aを正則と言います。
のとき、行列Aを正則と言います。
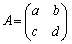 が逆行列をもつとき、2個のベクトル
が逆行列をもつとき、2個のベクトル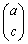 ,
,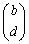 は1次独立です。
は1次独立です。
一般に、n次正方行列Aが逆行列をもつときには、行列Aを列ベクトルが横に並んだものと見て、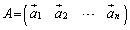 とすると、
とすると、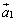 ,
,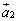 ,・・・,
,・・・,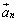 は1次独立です。
は1次独立です。
正方行列Aについて、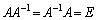 より、
より、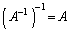 です。
です。
例.(1) 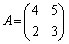 は、
は、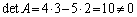 より、逆行列をもちます。
より、逆行列をもちます。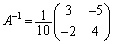
(2) 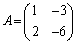 は、
は、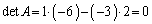 より、逆行列をもちません。
より、逆行列をもちません。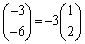 より、行列内の2個の列ベクトルは1次独立ではありません。
より、行列内の2個の列ベクトルは1次独立ではありません。
(3) 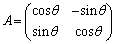 は、
は、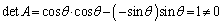 より、逆行列をもちます。
より、逆行列をもちます。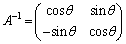
n次正方行列A,Bがともに逆行列をもつとき、
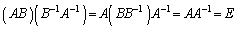
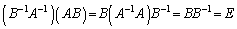
より、
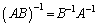
です。
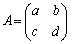 ,
,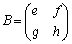 として、
として、
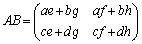
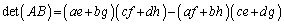
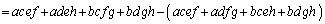
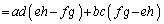
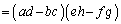
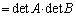
従って、A,Bのいずれかが逆行列を持たなければ(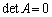 または
または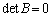 )、
)、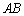 も逆行列を持ちません(
も逆行列を持ちません(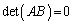 )。
)。
(3次以上の正方行列の逆行列について、どうしても知りたい人は、逆行列(その2)へ)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。