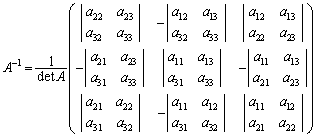�t�s��(����3)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�t�s��(����2)�̂Â��ł�
(6) ��A���ɂ́A��Ƌ�A���Ɗ���������Ƌ�ƂȂ�A��Ɗ��A���Ƌ��������Ɗ��ɂȂ�A�Ƃ�������������܂��B�]���āA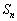 �ɑ�����2�̗v�fσ�Cτ������ꍇ�A
�ɑ�����2�̗v�fσ�Cτ������ꍇ�A
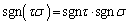
����āA�s��A�̗�����ւ���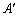 �ƂȂ�ꍇ�A��̓���ւ���\�������τ�Ƃ��āA
�ƂȂ�ꍇ�A��̓���ւ���\�������τ�Ƃ��āA
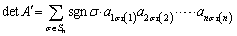
�@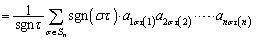
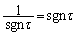 �ł���A����
�ł���A����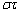 ��
��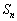 �̗v�f���ׂĂ��Ƃ�̂ŁA
�̗v�f���ׂĂ��Ƃ�̂ŁA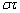 ��V����σ�Ə�����
��V����σ�Ə�����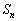 �̂��ׂĂ̗v�f�ɂ��đ������킹�邱�Ƃɂ���A
�̂��ׂĂ̗v�f�ɂ��đ������킹�邱�Ƃɂ���A
�@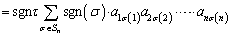
�@
(4)���A�s�ł́A��ɂ��Đ��藧���Ƃ͍s�ɂ��Ă����藧�̂ŁA�s��A�̍s�����ւ���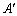 �ƂȂ�ꍇ�A�s��A�̍s�̓���ւ���\�������τ�Ƃ��āA
�ƂȂ�ꍇ�A�s��A�̍s�̓���ւ���\�������τ�Ƃ��āA
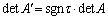
���ɁA�s��A�̑�j�s�Ƒ�k�s�����ւ���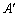 �ƂȂ�ꍇ�Aτ�͊��ɂȂ�̂ŁA
�ƂȂ�ꍇ�Aτ�͊��ɂȂ�̂ŁA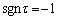 ���A
���A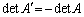 �ƂȂ�܂��B
�ƂȂ�܂��B
(7) �s��A�̑�j�s�Ƒ�k�s�����S�Ɉ�v���Ă����ꍇ�A��j�s�Ƒ�k�s�����ւ���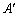 �ƂȂ��Ă��A
�ƂȂ��Ă��A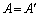 �C
�C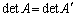 �ł��B
�ł��B
�ł����A���̂Ƃ�(6)���A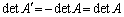
�� 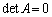
�܂�A�s��A�̒��ɁA���S�Ɉ�v���镡���̍s������Ƃ��ɂ́A�s�̒l��0�ł��B
�Ⴆ�A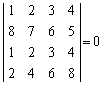 �@(��1�s�Ƒ�3�s����v)
�@(��1�s�Ƒ�3�s����v)
(8) �s��A�̑�j�s�ɑ�k�s�����������̂�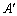 �Ƃ��āA
�Ƃ��āA
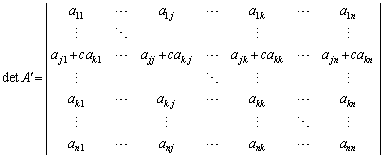
�@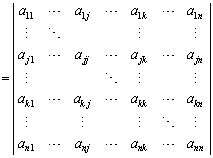
�@�@�@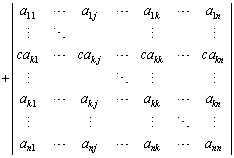
�@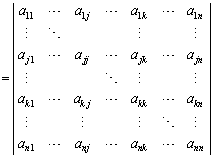
�@�@�@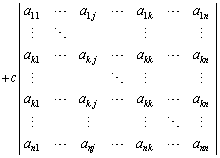
�@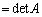 �@(�Ȃ��Ȃ�A��2���̍s�́A��j�s�Ƒ�k�s����v���Ă���0)
�@(�Ȃ��Ȃ�A��2���̍s�́A��j�s�Ƒ�k�s����v���Ă���0)
�܂�A�s��A�̑�j�s�ɑ�k�s�̒萔�{�������Ă��A�s�̒l�͕ω����܂���B
(9) 2�̍s��A�CB��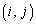 ������
������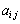 �C
�C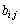 �Ƃ��āA�s��̐�
�Ƃ��āA�s��̐�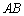 �̍s�́A
�̍s�́A
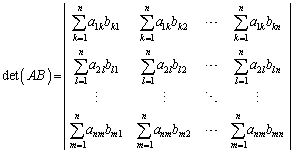
���̑�1�s�́A(5)�ɂ����āA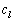 ��
��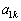 �ƂȂ����`�����Ă���̂ŁA���̂悤�ɏ��������܂��B
�ƂȂ����`�����Ă���̂ŁA���̂悤�ɏ��������܂��B
�@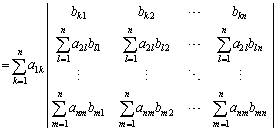
��2�s�����l�ɂ��āA(5)�ɂ����āA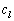 ��
��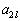 �ƂȂ����`�����Ă���̂ŁA
�ƂȂ����`�����Ă���̂ŁA
�@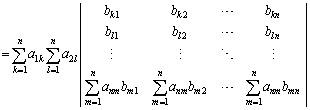
�ȉ��A��n�s�܂ł��ׂď��������ƁA
�@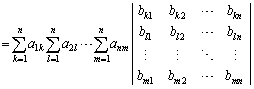 �@����@
�@����@
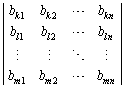 �ɂ��ẮA
�ɂ��ẮA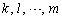 �̒��ɓ����ԍ����o�Ă���ƁA��1�s�����n�s�̒��ɁA���S�Ɉ�v���镡���̍s���܂ނ��ƂɂȂ�A(7)���s�̒l��0�ɂȂ�܂��B�]���āA�@�̃��ŁA�s�̒l��0�łȂ������c��̂́A
�̒��ɓ����ԍ����o�Ă���ƁA��1�s�����n�s�̒��ɁA���S�Ɉ�v���镡���̍s���܂ނ��ƂɂȂ�A(7)���s�̒l��0�ɂȂ�܂��B�]���āA�@�̃��ŁA�s�̒l��0�łȂ������c��̂́A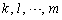 �����ׂĈقȂ鐔�ɂȂ�ꍇ�̂Ƃ��낾���ł��Bn�̐���
�����ׂĈقȂ鐔�ɂȂ�ꍇ�̂Ƃ��낾���ł��Bn�̐���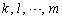 �����ׂĈقȂ�ꍇ�A
�����ׂĈقȂ�ꍇ�A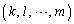 �́A
�́A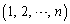 ����בւ�������ł�����
����בւ�������ł�����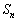 �̗v�f�ł��B
�̗v�f�ł��B
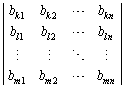 �́A
�́A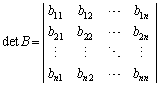 �̍s�����ւ����s�Ȃ̂ŁA
�̍s�����ւ����s�Ȃ̂ŁA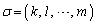 �Ƃ��āA(6)���A
�Ƃ��āA(6)���A
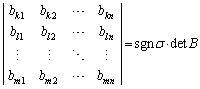
�@�ɑ������ƁAk�Cl�Cm�̃��̒��Ő����c���Ă���̂��A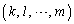 ��
��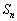 �̗v�f�ƂȂ�Ƃ��낾���ł��邱�Ƃɒ��ӂ���ƁA����
�̗v�f�ƂȂ�Ƃ��낾���ł��邱�Ƃɒ��ӂ���ƁA����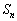 �̂��ׂĂ̗v�f�ɂ��Ă����Ƃ�悭�A
�̂��ׂĂ̗v�f�ɂ��Ă����Ƃ�悭�A
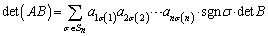
�@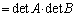
�ς̍s�́A�s�̐ςł��B
(10) n�������s��A��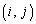 ������
������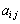 �Ƃ��܂��B�܂��A�s��A�̑�i�s�Ƒ�j�����菜���Ăł���
�Ƃ��܂��B�܂��A�s��A�̑�i�s�Ƒ�j�����菜���Ăł���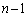 �������s��̍s��
�������s��̍s��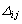 ��
��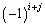 �����������̂��s��A�̑�
�����������̂��s��A�̑�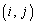 �]���q�ƌ����܂��B
�]���q�ƌ����܂��B
�s��A�̑�k�s���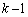 �s�Ɠ���ւ��A����ɁA��
�s�Ɠ���ւ��A����ɁA��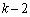 �s�Ɠ���ւ��A�Ƃ������Ƃ����āA�Ō�ɁA��1�s�����ւ���Ƃ��܂��B
�s�Ɠ���ւ��A�Ƃ������Ƃ����āA�Ō�ɁA��1�s�����ւ���Ƃ��܂��B
���̕��בւ�����σ�́Ak����Ȃ��Ak�������Ȃ���ɂȂ�܂��B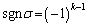
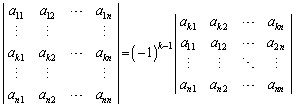 �@����A
�@����A
�s�̒�`(��)����A���̑�1�s���������̍s��̘a�ƍl���邱�Ƃɂ��A
�@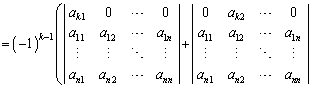
�@�@�@�@�@�@�@�@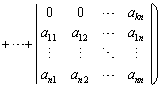
���̌�A��1�s��0�łȂ��v�f���܂ޗ���A�s�̓���ւ��Ɠ��l�ɂ��āA��1��܂ňڂ��܂��B��l����1��܂œ���ւ��Ă䂭�ƁA�s��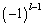 ��������܂��B
��������܂��B
�@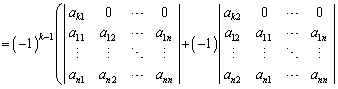
�@�@�@�@�@�@�@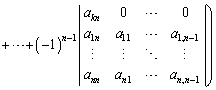
�@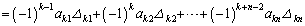
�� 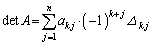 �@����B
�@����B
������A�s�̑�k�s�Ɋւ���W�J�ƌ����܂��B
��D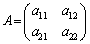 �ł́A��L�ɂ����āA
�ł́A��L�ɂ����āA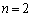 �C
�C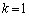 �Ƃ���ƁA
�Ƃ���ƁA
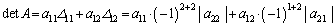
�@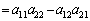
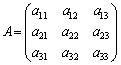 �ł́A��L(��)�ɂ����āA
�ł́A��L(��)�ɂ����āA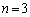 �C
�C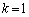 �Ƃ���ƁA
�Ƃ���ƁA
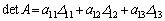
�@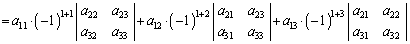
�@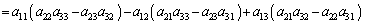
�@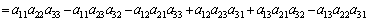
(11) (10)�B����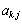 ��k��i�@(
��k��i�@(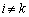 �C
�C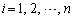 )�������Ƃ��Ă݂܂��B����͇A����k��i�ɕς��Ă݂�ƁA�A���E�ӂő�1�s�Ƒ�j�s���S����v���Ă��邱�Ƃ��Ӗ�����̂ŁA�A�̍s�̒l��0�ɂȂ�܂��B
)�������Ƃ��Ă݂܂��B����͇A����k��i�ɕς��Ă݂�ƁA�A���E�ӂő�1�s�Ƒ�j�s���S����v���Ă��邱�Ƃ��Ӗ�����̂ŁA�A�̍s�̒l��0�ɂȂ�܂��B
�܂�A �̂Ƃ��A
�̂Ƃ��A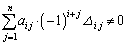
����ƇB�����킹�āA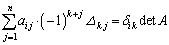
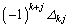 ��
��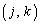 ����
����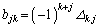 �Ƃ���s��(�]���q�s��ƌ����܂��B�E�ӂƍ��ӂ�j��k�̕��т�����ւ���Ă��邱�Ƃɒ��ӂ��Ă�������)���l����ƁA
�Ƃ���s��(�]���q�s��ƌ����܂��B�E�ӂƍ��ӂ�j��k�̕��т�����ւ���Ă��邱�Ƃɒ��ӂ��Ă�������)���l����ƁA
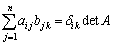
�]���q�s���B�Cn���̒P�ʍs���E�Ƃ���ƁA
�܂�A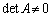 �ł���ꍇ�ɂ́A�s��A�͋t�s��
�ł���ꍇ�ɂ́A�s��A�͋t�s��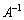 �������A
�������A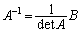
����āAn�������s��A�̋t�s��́AA�̗]���q�s���A�̍s�Ŋ��������́A�Ƃ������ƂɂȂ�܂��B
�܂��An�������s��A�ɂ����Ă��AA������(�t�s�������) �� 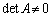
��D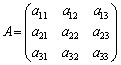 �̗]���q�s��́A
�̗]���q�s��́A
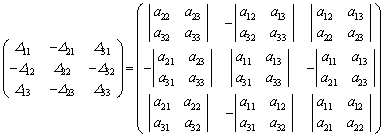
����āA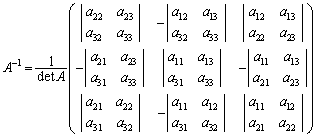
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 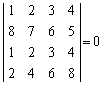 �@(��1�s�Ƒ�3�s����v)
�@(��1�s�Ƒ�3�s����v)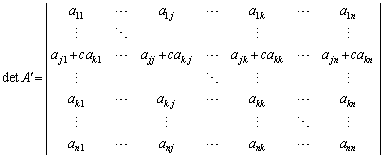
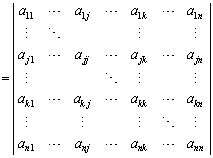
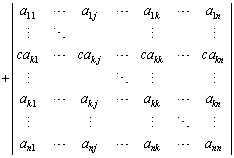
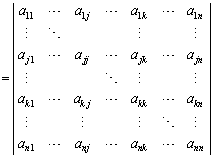
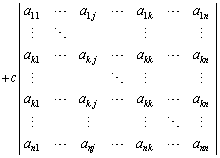
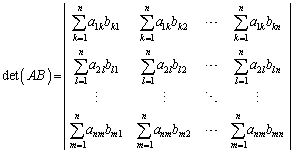
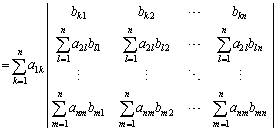
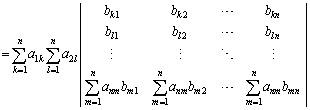
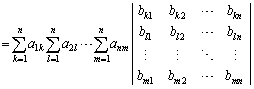 �@����@
�@����@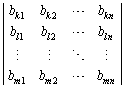 �ɂ��ẮA
�ɂ��ẮA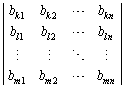 �́A
�́A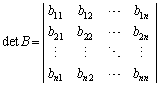 �̍s�����ւ����s�Ȃ̂ŁA
�̍s�����ւ����s�Ȃ̂ŁA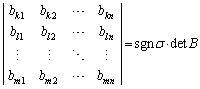
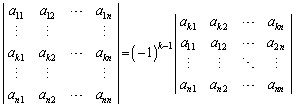 �@����A
�@����A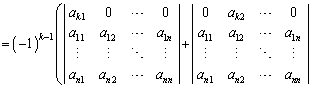
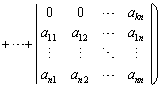
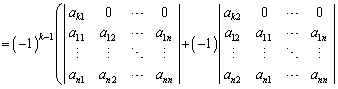
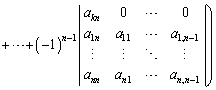
 �ł́A��L(��)�ɂ����āA
�ł́A��L(��)�ɂ����āA �̗]���q�s��́A
�̗]���q�s��́A