微分方程式 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理への応用(その2)という項目の中に、
一定の力と速度に比例する抵抗力を受けて運動する物体に関する関係式として
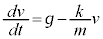 ・・・①
・・・①
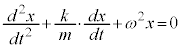 ・・・②
・・・②
①の場合には、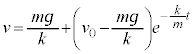 が、微分方程式①の解になります。
が、微分方程式①の解になります。
②の場合には、例えば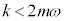 の場合には、
の場合には、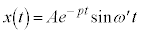 (ただし、
(ただし、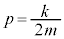 ,
,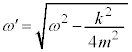 ) が解になります。
) が解になります。
このように、微分方程式では、微分方程式を満たす関数が解になります。
微分方程式では、微分方程式を満たす関数を求めることを、「微分方程式を解く」と言います。
微分方程式を解く際に、不定積分の計算が出てくるのですが、不定積分を行うと積分定数が出てきます。この積分定数の値を確定するために、時刻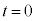 における速度の値や、x座標の値を指定したりします(何をどう指定するかは問題ごとに異なります)。積分定数の値を指定するための条件を初期条件(ある時刻における関数値、導関数値などを指定)、境界条件(ある位置における関数値、導関数値などを指定)などと言います。
における速度の値や、x座標の値を指定したりします(何をどう指定するかは問題ごとに異なります)。積分定数の値を指定するための条件を初期条件(ある時刻における関数値、導関数値などを指定)、境界条件(ある位置における関数値、導関数値などを指定)などと言います。
微分方程式でもっとも簡単なものは、
というタイプです。
これは、右辺をxで積分することにより、即座にyが求まります。つまり、
[解答] 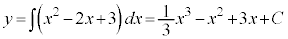 (Cは積分定数)
(Cは積分定数)
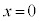 のとき、
のとき、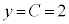
∴ 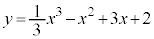 ......[答]
......[答]
次に簡単なタイプは、
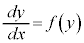 ・・・③
・・・③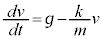 は、このタイプです。
は、このタイプです。
物理への応用(その2)という項目においては、逆関数の微分法の公式を用いて、
としたのですが、これを、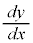 を分数のように扱い、③を形式的に次のように式変形します。
を分数のように扱い、③を形式的に次のように式変形します。
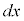 を右辺に移項し、
を右辺に移項し、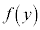 を左辺に移項(
を左辺に移項(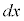 を両辺にかけ、
を両辺にかけ、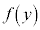 で両辺を割るという感覚です)し、
で両辺を割るという感覚です)し、
という形を作って、両辺に積分記号をつけます。
とします。
例2. ①を、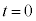 のとき
のとき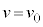 という初期条件のもとに、この形式で解くと、
という初期条件のもとに、この形式で解くと、 [解答] 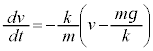
ここで、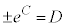 と置き直すと、
と置き直すと、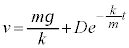
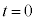 のとき、
のとき、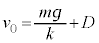
∴ 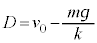 ∴
∴ 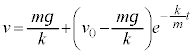 ......[答]
......[答] 注.厳格には、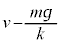 で割るので、
で割るので、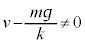 という確認が必要です。この問題では、初期条件に
という確認が必要です。この問題では、初期条件に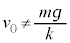 という条件が必要になります。
という条件が必要になります。
③をもう少し複雑にしたものに変数分離型と呼ばれるタイプがあります。これは、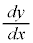 がxのみの関数
がxのみの関数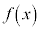 とyのみの関数
とyのみの関数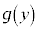 の積の形に表せるというものです。つまり、
の積の形に表せるというものです。つまり、
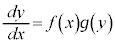
両辺に形式的に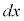 をかけ、
をかけ、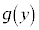 で割ります。
で割ります。
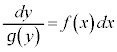
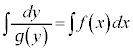
ここから、関数を求めます。
例3. a,bを与えられた正の定数とする。cがいろいろな値をとることにより得られる曲線群: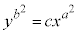 の曲線のすべてと直交する曲線を求める。但し、求める曲線は点
の曲線のすべてと直交する曲線を求める。但し、求める曲線は点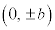 を通過する曲線であるとする。
を通過する曲線であるとする。 [解答] 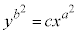 両辺をxで微分すると、
両辺をxで微分すると、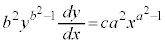 ・・・④
・・・④
求めたい曲線は、ある特定のcの値に対する1つの曲線と直交するのではなく、cがいろいろな値をとることにより得られる曲線群のすべてと直交するので、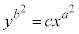 を用いてcを消去します。
を用いてcを消去します。
∴ 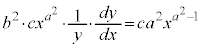
∴ 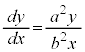
この式は、曲線群に属する曲線の点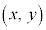 における接線の傾きが
における接線の傾きが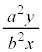 であることを意味しています。
であることを意味しています。
従って、これと直交する曲線の同じ座標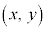 における接線の傾きは、
における接線の傾きは、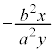 でなければなりません。
でなければなりません。
従って、求める曲線について、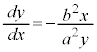 が成立します。
が成立します。
両辺に形式的に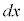 をかけ、xで割ると、
をかけ、xで割ると、
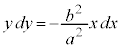
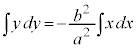
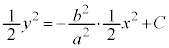 (Cは積分定数)
(Cは積分定数)
両辺に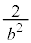 をかけて、
をかけて、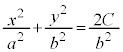
これは楕円です。
この問題に関する限り、もとの曲線群に属する曲線の一つが、y軸に一致することはあり得ないので、楕円のy軸上の点は除きます。
この楕円が、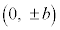 を通過するような楕円である場合には、
を通過するような楕円である場合には、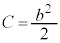 となります。求める曲線は、楕円:
となります。求める曲線は、楕円: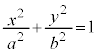 (但し、
(但し、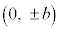 を除く)となります。
を除く)となります。
もとの曲線群が、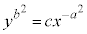 だったとすると、
だったとすると、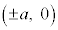 を通過するのなら
を通過するのなら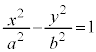 、
、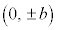 を通過するのなら
を通過するのなら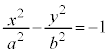 という双曲線になります。
という双曲線になります。
注.ある曲線群に属するずべての曲線と直交する曲線を直交截線と言います。物理の電磁気で出てくる、すべての電気力線と垂直な等電位線がこれにあたります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 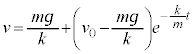 が、微分方程式①の解になります。
が、微分方程式①の解になります。 ) が解になります。
) が解になります。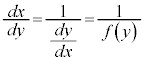
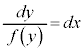
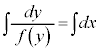
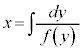 (積分定数は、
(積分定数は、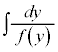 にまとめます)
にまとめます)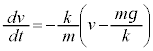
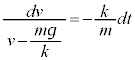
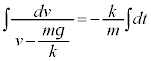
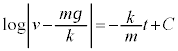 (Cは積分定数)
(Cは積分定数)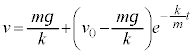 ......[答]
......[答]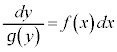
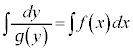
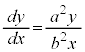
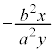 でなければなりません。
でなければなりません。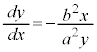 が成立します。
が成立します。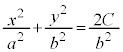
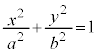 (但し、
(但し、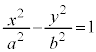 、
、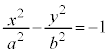 という双曲線になります。
という双曲線になります。