�����ւ̉��p(����2)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����ւ̉��p�̑����ł��B
�Ȍ�͈ꎟ���̉^�����l���܂��B
�����~�^�����镨�̂�y���ɐ����ȕ���������Ă�y���ɕ��̂̉e�����Ƃ��A�e���s���^����P�U���ƌ����܂��B
���̂̈ʒu��y���W�́A
���̂̑��x�́A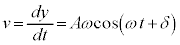
���̂̉����x�́A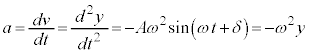
�^���������́A�͂�f�Ƃ���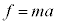 �ƂȂ�܂����A
�ƂȂ�܂����A
 ���̗�
���̗�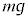 ���ē������x�^�����Ă��镨�̂��A����ɁA���x�ɔ�Ⴗ���R��
���ē������x�^�����Ă��镨�̂��A����ɁA���x�ɔ�Ⴗ���R��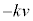 (k��萔)�������Ƃ��^���������́A
(k��萔)�������Ƃ��^���������́A
�t���̔����@�̌������A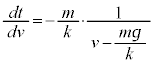
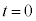 �̂Ƃ��̑��x��
�̂Ƃ��̑��x��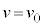 ���Ƃ��āA
���Ƃ��āA
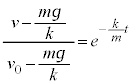 ��
�� 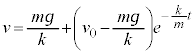
 �̂Ƃ��A
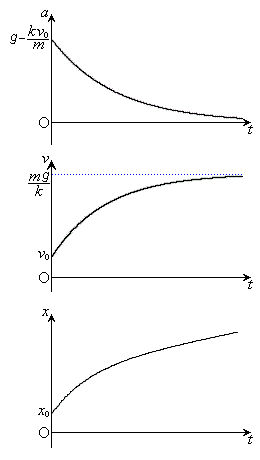
�̂Ƃ��A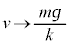 �ƂȂ�A���̂̉^���͓����x�^���ɋ߂Â��Ă����܂��B���̍ŏI�I�ȑ��x
�ƂȂ�A���̂̉^���͓����x�^���ɋ߂Â��Ă����܂��B���̍ŏI�I�ȑ��x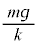 ���I�[���x�ƌ����܂��B
���I�[���x�ƌ����܂��B
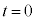 �̂Ƃ��A
�̂Ƃ��A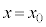 ���Ƃ��āA
���Ƃ��āA
�����xa�C���xv�C���Wx�̎���t�ɑ���W���E�}�Ɏ����܂��B
�P�U�����Ă��镨��(���Wx)�ɁA���xv�ɔ�Ⴗ���R�������ƁA�^���������́A
2���������F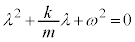 �@����A
�@����A
�A�̔��ʎ��F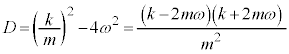
(i) 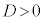 �C�܂�A
�C�܂�A �̂Ƃ�(��R�͂��������Ƃ��Ӗ����܂�)�A
�̂Ƃ�(��R�͂��������Ƃ��Ӗ����܂�)�A �A�́A2�̎������F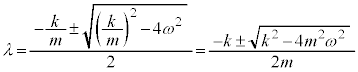 2���Ƃ����̉��ŁA
2���Ƃ����̉��ŁA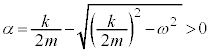 �C
�C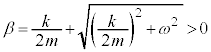 �Ƃ��āA2���́A
�Ƃ��āA2���́A �C
�C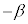 �ƂȂ�܂��B
�ƂȂ�܂��B
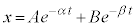 �Ƃ����ƁA
�Ƃ����ƁA �@�̍��ӂɑ������ƁA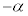 �C
�C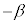 �́A�A�̉�������A
�́A�A�̉�������A �ƂȂ�A�@�����̂ŁA���̂̍��W�́A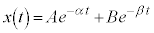 �ƂȂ�܂��B
�ƂȂ�܂��B (ii) 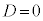 �C�܂�A
�C�܂�A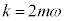 �̂Ƃ�(��R�͂͂��傤�ǂ悢�Ƃ�)�A
�̂Ƃ�(��R�͂͂��傤�ǂ悢�Ƃ�)�A ���̂Ƃ��A�A�͏d��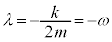 �������܂��B
�������܂��B
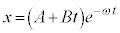 �Ƃ����ƁA
�Ƃ����ƁA �@�̍��ӂɑ������ƁA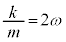 ���A
���A �ƂȂ�A�@�����̂ŁA���̂̍��W�́A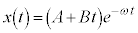 �@����B
�@����B (iii) 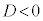 �C�܂�A
�C�܂�A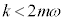 �̂Ƃ�(��R�͂��������Ƃ�)�A
�̂Ƃ�(��R�͂��������Ƃ�)�A 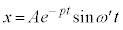 �Ƃ����ƁA
�Ƃ����ƁA�@�ɑ������ƁA
���ꂪ�P���I�ɐ��藧�ꍇ�A
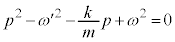 �@����C�C
�@����C�C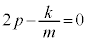 �@����D
�@����D�D���A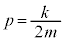
�C���A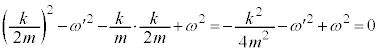
�� 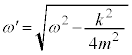 �@(�������͐�)
�@(�������͐�)
��w�����ɏo�肳�����ŁA������A�e��ɐ��𗬓���������A�e�킩�琅�𗬏o������Ƃ�����肪����܂��B
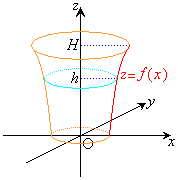 �����ł́A�E�}�̂悤�ɁA�P�������Ȋ��Ƃ��ė^������Ȑ��F
�����ł́A�E�}�̂悤�ɁA�P�������Ȋ��Ƃ��ė^������Ȑ��F ��z���̉���1��]���ē�����Ȗʂ�e�푤�ʂƂ��Axy���ʏ�ɒ�ʂ����e��ɁA�ォ�琅�𗬓������邱�Ƃ��l���܂��B
��z���̉���1��]���ē�����Ȗʂ�e�푤�ʂƂ��Axy���ʏ�ɒ�ʂ����e��ɁA�ォ�琅�𗬓������邱�Ƃ��l���܂��B
���낢��ȓ�����肪�l�����܂����A�����ł́A���̗������x��K�ň��A�e��̐[����H���Ƃ��āA����0���琅�����n�߂ėe�킪���t�ɂȂ�܂ł̎���T�Ɛ��[h�̕ω���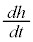 �����߂Ă݂܂��B
�����߂Ă݂܂��B
�e���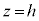 �Ő����Ƃ��̒f�ʂ̉~�̖ʐς́A
�Ő����Ƃ��̒f�ʂ̉~�̖ʐς́A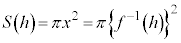
���[��h�ɂȂ����Ƃ��̗e����̐��̗ʂ́A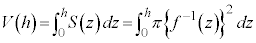 �@(y���̉��̉�]�����Q��)
�@(y���̉��̉�]�����Q��)
���̗������x�́A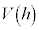 ��t�Ŕ������āA
��t�Ŕ������āA
���ꂪK�ɓ������̂ŁA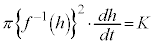
�]���āA���[�̕ω����́A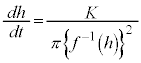 �ƂȂ�܂��B
�ƂȂ�܂��B
���āA���̎���p����h��t�̎��ŕ\�������̂ł����A���̂܂܂ł́A�E�ӂ�t�Őϕ��ł��܂���B
�����ŁA�t���̔����@�ɂ��A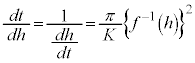
����ŗ��ӂ�h�Őϕ����邱�Ƃɂ��A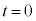 �ɂ�����
�ɂ�����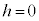 ���A
���A
���t�ɂȂ�Ƃ��A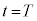 �ɂ����āA
�ɂ����āA ���A
���A
�Ⴆ�A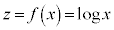 �ƂȂ�ꍇ�ł́A
�ƂȂ�ꍇ�ł́A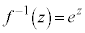 ���A
���A
���[�̕ω����́A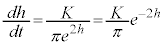
���t�ɂȂ�܂ł̎��Ԃ́A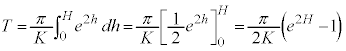 �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 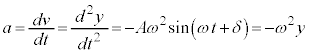
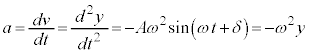
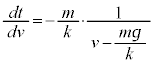
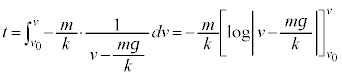
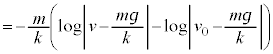
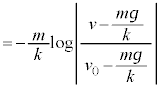
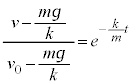
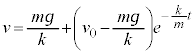
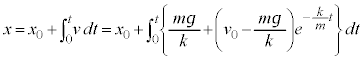
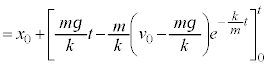
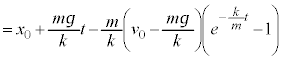
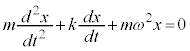 �@(
�@(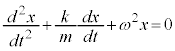 �@����@
�@����@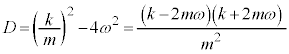
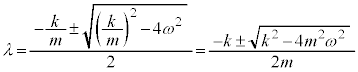
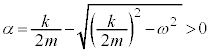 �C
�C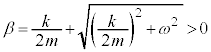 �Ƃ��āA2���́A
�Ƃ��āA2���́A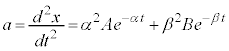
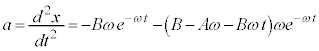
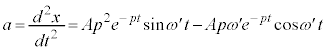
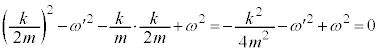
 �@(�������͐�)
�@(�������͐�)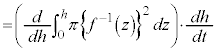
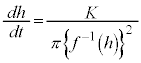 �ƂȂ�܂��B
�ƂȂ�܂��B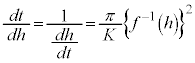
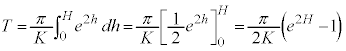 �ł��B
�ł��B