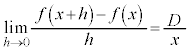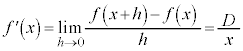��ϕ��Ɣ��� ( ���� 2) �@�@�@ �֘A��� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂł́A ��ϕ��Ɣ��� ���Q�Ƃ��Ă��������B [ �ؖ� ] �@ x �Ŕ�������ƁA ( �ؖ��I ) �� 1 �D�@ t �Ɋւ���ϕ����s���ۂɁA��ϕ����ɁA t �ȊO�̕��� (t �Ƃ̈ˑ��W���Ȃ� ) ���܂ޏꍇ�ɂ́A���̕�����ϕ��v�Z�����s����Ƃ��ɂ͒萔�ƌ��Ȃ��Čv�Z ( �Ȃ�ׂ��ϕ��̊O���ɏo���悤�ɂ��� ) ���A���̌�ɔ����̌v�Z���s���悤�ɂ��܂��B 2 �D�@ x ��ϕ��̊O�ɏo�����߂ɁA �u���ϕ� ���܂��B t �F u �F �@ 3 �D�@ [ �� ] �@ ( �����ϕ� ���Q�� ) �B�ɑ�����āA �A�ɑ������ƁA .......[ �� ] ��ϕ����܂ޓ������^�����Ċ������߂���ŁA��ϕ��̏�[�܂��͉��[���ϐ��ɂȂ��Ă���ꍇ�ɂ́A���L�̂悤�ɂ��܂��B (i) ��ϕ��̏�[�Ɖ��[���������Ȃ� ( ���̂Ƃ���ϕ��̒l�� 0 �ł� ) �悤�ȁA�ϐ��̒l���A�^����ꂽ�����ɑ�����܂��B���炩�̏������������܂��B (ii) ��ϕ���������悤�ɁA��ϕ��̏�[�܂��͉��[�ɏo�Ă���ϐ��Ŕ������܂��B�����v�Z���K�v�ł����A����ŁA���߂���̎�v���������܂�܂��B�Ō�� (i) �œ���ꂽ���������g���āA�����m�肵�܂��B 4 �D�@ [ �� ] �@�^���ŁA ( ��ϕ��� 0 �ɂ��� ) �ƁA x �Ŕ�������ƁA ���ӂ� x �Őϕ�����ƁA ( �s��ϕ��̌��� ���Q�� ) �� �� �Ƃ����ƁA �� �� ] �� 5 �D�@ x �C y �ɂ��āA�����F [ �� ] �@�����Ȃ�A�^����ꂽ�����F ���� �̌����F h ���Ƃ�A�@�ɑ������ƁA �@����A �����W�� �́A �����\ �Ƃ������Ƃ́A���̋Ɍ��͋Ɍ��l�����A�Ƃ������Ƃł��B ����āA�A���A ( �� �C ) �Ƃ����āA x �ɂ����Ĕ����\�ŁA x �Őϕ�����ƁA ( ���A �� ] �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@ ���w��b���� TOP �@�@ ���w TOP �@�@ TOP �y�[�W�ɖ߂� �y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B �e���̒��쌠�� © 2005-2024 (�L)����� ��w�y�w�m ���������t���I ���n��w�l�b�g�m ��w�y�w�m (���ē��������� )������́A������܂Ń��[�� �� 
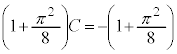
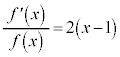
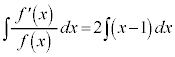 �@(�s��ϕ��̌������Q��)
�@(�s��ϕ��̌������Q��)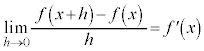 �𗘗p���邱�Ƃ��l���܂��B
�𗘗p���邱�Ƃ��l���܂��B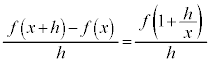 �@����A
�@����A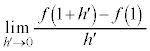 �Ƃ����`�����Ă��܂����A
�Ƃ����`�����Ă��܂����A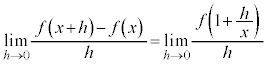
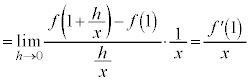 �@(��
�@(��