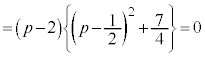��ϕ��Ɣ����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
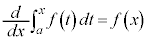
[�ؖ�]�@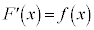 ���Ƃ��܂��B
���Ƃ��܂��B
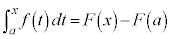 �@(��ϕ����Q��)
�@(��ϕ����Q��)
���ӂ�x�����������ƁA
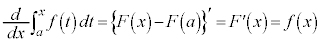 �@(�ؖ��I)
�@(�ؖ��I)
��D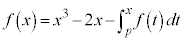 ����2����
����2����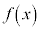 �Ǝ����̒萔p�����߂�B
�Ǝ����̒萔p�����߂�B
[��]�@��ϕ��̏�[��x�ɂȂ��Ă���̂ŁA��ϕ��͒萔�ł͂Ȃ�x�̊��ł��B
��ϕ��ɂ͏�[�Ɖ��[���������Ƃ���0�ɂȂ�Ƃ�������������̂ŁA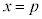 ��^���ɑ�����āA��ϕ���0�ɂȂ�悤�ɂ��Ă݂�ƁA
��^���ɑ�����āA��ϕ���0�ɂȂ�悤�ɂ��Ă݂�ƁA
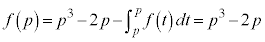 �@����@
�@����@
�܂��A��L�̒藝�ɂ��A�^�����ӂ�x�Ŕ������Ă݂�ƁA
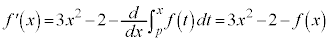 �@�E�E��A
�@�E�E��A
2����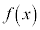 ��
��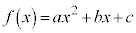 �Ƃ����ƁA
�Ƃ����ƁA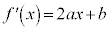
�A�ɑ�����āA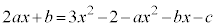
��������ƁA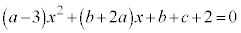
���ꂪ�C�ӂ̎���x�Ő��藧���߂�(�P�������Q��)�A
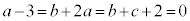
�� 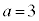 �C
�C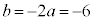 �C
�C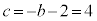
����āA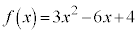
�@���A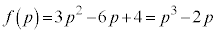
�� 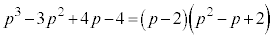
�@�@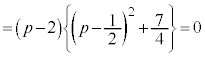
���J�b�R���͐��ŁA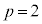
�ȏ���A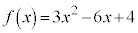 �C
�C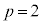 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B