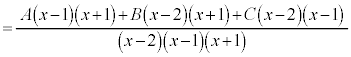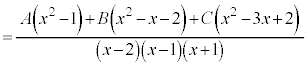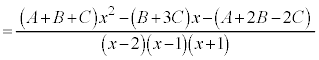�P�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
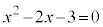 �Ƃ��������́A
�Ƃ��������́A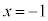 ��
��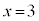 �̂Ƃ��Ɍ����Đ��藧���ł��B�����x�̒l�ɂ��Ă������藧����������ƌ����܂��B
�̂Ƃ��Ɍ����Đ��藧���ł��B�����x�̒l�ɂ��Ă������藧����������ƌ����܂��B
����ɑ��āA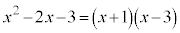 �Ƃ��������́Ax�ɂ����Ȃ�����������Ă����藧���܂��B���̂悤�ȓ������P�����ƌ����܂��B
�Ƃ��������́Ax�ɂ����Ȃ�����������Ă����藧���܂��B���̂悤�ȓ������P�����ƌ����܂��B
�������A�P�����ɂ���ẮA���Ƃ��ĈӖ��������Ȃ�x�̒l(�����0�ɂ���x�C�������ɂ���x�Ȃ�)�������čl������̂�����܂��B
(�������E�s�������Q��)
��1�D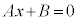 ��x�ɂ��Ă̍P���� ��
��x�ɂ��Ă̍P���� �� 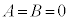
[�ؖ�]�@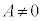 ���Ƃ���ƁA
���Ƃ���ƁA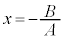 �ƂȂ�A�����F
�ƂȂ�A�����F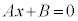 ����x�̒l������1�Ɋm�肵�Ă��܂��܂��B����ł́A
����x�̒l������1�Ɋm�肵�Ă��܂��܂��B����ł́A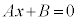 ���P�����ɂȂ�Ȃ��̂ŁA
���P�����ɂȂ�Ȃ��̂ŁA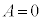 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A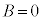
�t�ɁA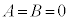 �̂Ƃ��A�C�ӂ̎���x�ɂ��āA
�̂Ƃ��A�C�ӂ̎���x�ɂ��āA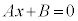 �ł��B�@(�ؖ��I)
�ł��B�@(�ؖ��I)
��2�D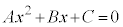 ��x�ɂ��Ă̍P���� ��
��x�ɂ��Ă̍P���� �� 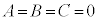
[�ؖ�]�@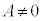 ���Ƃ��܂��B
���Ƃ��܂��B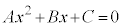 ����@ ���A�C�ӂ̎���x�ɂ��Đ������邩��A�قȂ�3�̒l�A
����@ ���A�C�ӂ̎���x�ɂ��Đ������邩��A�قȂ�3�̒l�A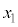 �C
�C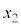 �C
�C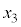 ��x�ɑ�������Ƃ��ɇ@���������܂��B����́A2���������@�̑��قȂ���̐������X2�ł���Ƃ��������ɔ����܂��B����āA
��x�ɑ�������Ƃ��ɇ@���������܂��B����́A2���������@�̑��قȂ���̐������X2�ł���Ƃ��������ɔ����܂��B����āA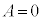
���̂Ƃ��A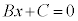
��1�D�ɂ��A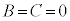 �C����āA
�C����āA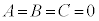
�t�ɁA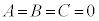 �̂Ƃ��ɁA
�̂Ƃ��ɁA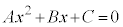
��2�D�̏ؖ������̂悤�ɍs�����Ƃ��ł��܂��B�u�C�ӂ�......�v�Ƃ����\��������Ƃ��ɁA�������̒l�ɂ��Đ��藧�Ƃ��āA�ȒP�ȏꍇ����������o���Ƃ����Z�I�́A�Z�I�Ƃ��āA�������U������Ƃ��ɂ����Ύg����d�v�Z�I�ł��B
[��2�D�̏ؖ�]�@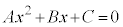 ����@ ���C�ӂ̎���x�Ɋւ��Đ��藧�̂�����A
����@ ���C�ӂ̎���x�Ɋւ��Đ��藧�̂�����A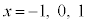 �ɂ����Ă����藧�B
�ɂ����Ă����藧�B
�@�ɂ����āA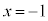 �Ƃ���ƁA
�Ƃ���ƁA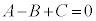 ����A
����A
�@�ɂ����āA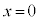 �Ƃ���ƁA
�Ƃ���ƁA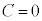 ����B
����B
�@�ɂ����āA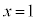 �Ƃ���ƁA
�Ƃ���ƁA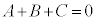 ����C
����C
�B���A�ɑ������ƁA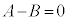
�� 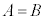 ����D
����D
�B�C�D���C�ɑ������ƁA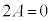
�� 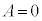
�D���A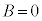
����āA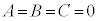
���ꂾ���ł́A�ؖ��ɂȂ��Ă��܂���B�Ȃ��Ȃ�Ax�̓��ʂȒl�A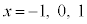 �ɂ��Ă������ׂĂ��Ȃ�����ł��B
�ɂ��Ă������ׂĂ��Ȃ�����ł��B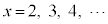 �Ƃ��Ă����Ɛ��藧���Ȃ������m��܂���B
�Ƃ��Ă����Ɛ��藧���Ȃ������m��܂���B
��ł���Ă������Ƃ́A�g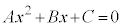 ��x�ɂ��čP���� ��
��x�ɂ��čP���� �� 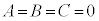 �h�C�܂�A�g
�h�C�܂�A�g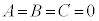 �h���A�g
�h���A�g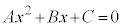 ��x�ɂ��čP�����h���K�v�����ł��邱�Ƃ��������ɉ߂��Ȃ��̂ł��B
��x�ɂ��čP�����h���K�v�����ł��邱�Ƃ��������ɉ߂��Ȃ��̂ł��B
�]���āA�g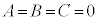 �h���A�g
�h���A�g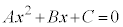 ��x�ɂ��čP�����h���\�������ł��邱�Ƃ������Ȃ��ƁA�g
��x�ɂ��čP�����h���\�������ł��邱�Ƃ������Ȃ��ƁA�g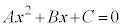 ��x�ɂ��čP���� ��
��x�ɂ��čP���� �� 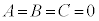 �h (���L�����A�e��'�����e��'�ɕς���Ă��邱�Ƃɒ���)�����������ƂɂȂ�Ȃ��̂ł��B
�h (���L�����A�e��'�����e��'�ɕς���Ă��邱�Ƃɒ���)�����������ƂɂȂ�Ȃ��̂ł��B
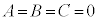 �ł���A
�ł���A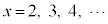 �ł������Ƃ��Ă��A�@�����藧���Ƃ��������߂ɁA�ȉ���1�s���ؖ��ɂ��Ă����K�v������܂��B
�ł������Ƃ��Ă��A�@�����藧���Ƃ��������߂ɁA�ȉ���1�s���ؖ��ɂ��Ă����K�v������܂��B
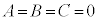 �ł���A
�ł���A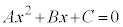 ��x�ɂ��čP�����B�@(�ؖ��I)
��x�ɂ��čP�����B�@(�ؖ��I)
�ȏ�̏ؖ��ŁA�Ȃ��A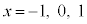 �ɂ����̂��H�Ƃ����^������l�����邩���m��܂���B�ʂɁA
�ɂ����̂��H�Ƃ����^������l�����邩���m��܂���B�ʂɁA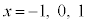 �łȂ���Ȃ�Ȃ��Ƃ������Ƃ͂���܂���B
�łȂ���Ȃ�Ȃ��Ƃ������Ƃ͂���܂���B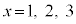 �ł����Ă��\���܂���B�ł����A�킴�킴�A
�ł����Ă��\���܂���B�ł����A�킴�킴�A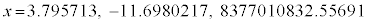 �̂Ƃ��A�ȂǂƂ��ƁA�l�������_�ɉ߂������ƂɂȂ�܂�(���܂ɂ͎��ԂԂ��ʼn�蓹���C���炵�ɂ��������m��܂��A�������ł͕s�ł�)�B�܂�A
�̂Ƃ��A�ȂǂƂ��ƁA�l�������_�ɉ߂������ƂɂȂ�܂�(���܂ɂ͎��ԂԂ��ʼn�蓹���C���炵�ɂ��������m��܂��A�������ł͕s�ł�)�B�܂�A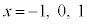 �ɂ��Ă���̂́A�A����������f�����������߂ł��B
�ɂ��Ă���̂́A�A����������f�����������߂ł��B
��3�D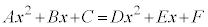 ��x�ɂ��Ă̍P���� ��
��x�ɂ��Ă̍P���� �� 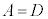 ����
���� 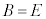 ����
���� 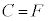
[�ؖ�]�@ 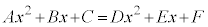 ��x�ɂ��Ă̍P����
��x�ɂ��Ă̍P����
�� 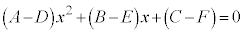 ��x�ɂ��Ă̍P����
��x�ɂ��Ă̍P����
�� 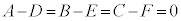 �@(��2�D���)
�@(��2�D���)
�� 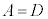 ����
���� 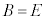 ����
���� 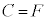 �@(�ؖ��I)
�@(�ؖ��I)
��4�D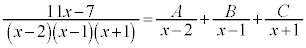 ��x�ɂ��čP�����ƂȂ�悤��x�̒l���߂�B
��x�ɂ��čP�����ƂȂ�悤��x�̒l���߂�B
[��]�@�E�ӂ�ʕ����ĕ���𑵂�����ŁA���q����L�̍P�����̏��������悤�ɂ��܂��B
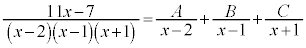
�@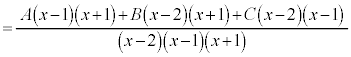
�@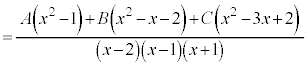
�@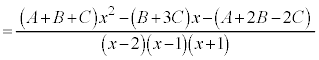
���ꂪx�ɂ��čP�����ƂȂ邽�߂ɁA���q���r���āA
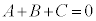 ����@�C
����@�C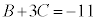 ����A�C
����A�C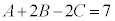 ����B
����B
�B�|�@���A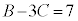 ����C
����C
�A�|�C���A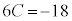
�� 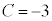
�A���A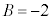
�@���A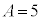
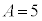 �C
�C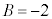 �C
�C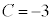 ......[��]
......[��]
(1) 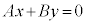 ���A�C�ӂ̎���x�Cy�ɂ��Đ������� ��
���A�C�ӂ̎���x�Cy�ɂ��Đ������� �� 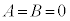
(2) 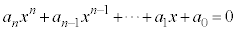 ���C�ӂ̎���x�ɂ��Đ�������
���C�ӂ̎���x�ɂ��Đ�������
�@�� 
(3) 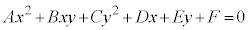 ���A�C�ӂ̎���x�Cy�ɂ��Đ������� ��
���A�C�ӂ̎���x�Cy�ɂ��Đ������� �� 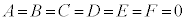
(4) 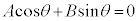 ���A�C�ӂ̎���θ�ɂ��Đ�������@�́@
���A�C�ӂ̎���θ�ɂ��Đ�������@�́@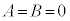
[�ؖ�](1) 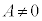 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA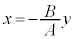 �ƂȂ�y��1�̒l�ɑ���x�̒l��1�Ɋm�肵�Ă��܂��܂��B
�ƂȂ�y��1�̒l�ɑ���x�̒l��1�Ɋm�肵�Ă��܂��܂��B
����ł́A�C�ӂ̎���x�Cy�ɂ���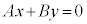 ����������Ƃ��������ɔ����܂��B
����������Ƃ��������ɔ����܂��B
�� 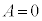 �C
�C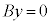
y��0�ȊO�̒l����蓾��̂ŁA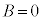 �C����āA
�C����āA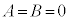
�t�ɁA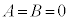 �̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA
�̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA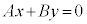 ���������܂��B�@(�ؖ��I)
���������܂��B�@(�ؖ��I)
(2) 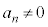 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA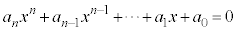 ����@ ���C�ӂ̎���x�ɂ��Đ������邩��A���قȂ�
����@ ���C�ӂ̎���x�ɂ��Đ������邩��A���قȂ�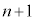 �̎���
�̎���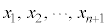 �ɂ��ć@���������܂��B����́An���������@�̑��قȂ�������Xn�ł���Ƃ��������ɔ����܂��B
�ɂ��ć@���������܂��B����́An���������@�̑��قȂ�������Xn�ł���Ƃ��������ɔ����܂��B
�� 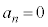
�ȉ��A���l�ɂ��āA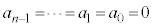
�t�ɁA �̂Ƃ��A���炩�ɁA�C�ӂ̎���x�ɂ��āA
�̂Ƃ��A���炩�ɁA�C�ӂ̎���x�ɂ��āA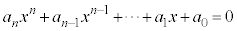 ���������܂��B�@(�ؖ��I)
���������܂��B�@(�ؖ��I)
(3) 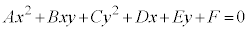 ��x�ɂ��Đ�������ƁA
��x�ɂ��Đ�������ƁA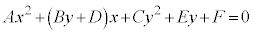
���̓������C�ӂ̎���x�ɂ��Đ������邩��A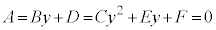
���ł��C�ӂ̎���y�ɂ��Đ������邩��A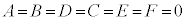
�t�ɁA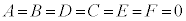 �̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA
�̂Ƃ��A���炩�ɁA�C�ӂ̎���x�Cy�ɂ��āA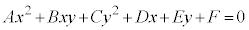 ���������܂��B�@(�ؖ��I)
���������܂��B�@(�ؖ��I)
(4) 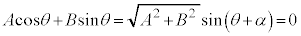 �Cα�́A
�Cα�́A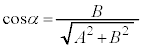 �C
�C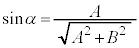 �����p�B
�����p�B
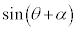 ��
��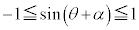 �ł��邢�낢��Ȓl���Ƃ�̂ŁA
�ł��邢�낢��Ȓl���Ƃ�̂ŁA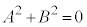 �@��
�@�� 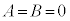
�t�ɁA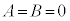 �̂Ƃ��A
�̂Ƃ��A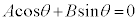 �@(�ؖ��I)
�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B