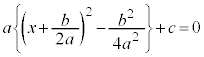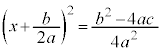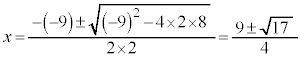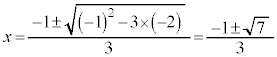2���������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�܂��A�ȒP��2���������F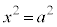 ���l���Ă݂܂��B
���l���Ă݂܂��B
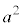 ���ڍ����āA������������ƁA
���ڍ����āA������������ƁA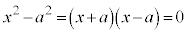
2�̎���α�Cβ ������Ƃ��A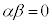 ���Ƃ���ƁAα��β �̂ǂ��炩��0�ł��B
���Ƃ���ƁAα��β �̂ǂ��炩��0�ł��B
�Ȃ��Ȃ�A�ǂ����0�łȂ��Ƃ���A�܂�A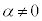 �C
�C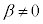 ���Ƃ���A
���Ƃ���A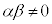 ������ł��B
������ł��B
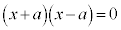 �Ƃ������Ƃ́A
�Ƃ������Ƃ́A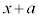 ��
��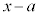 �̂ǂ��炩��0�ł��B
�̂ǂ��炩��0�ł��B
�܂�A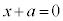 �C�܂��́A
�C�܂��́A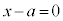
�]���āA �C�܂��́A
�C�܂��́A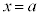
�����1�ɂ܂Ƃ߂āA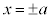 �̂悤�ɏ����܂��B'�}'�������ƌ����܂��B
�̂悤�ɏ����܂��B'�}'�������ƌ����܂��B
�ȏ���A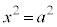 �̉��́A
�̉��́A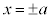 �ł��B ���(��)
�ł��B ���(��)
2���������F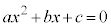 (
(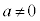 ) ����@
) ����@
�܂��A���ӂɂ��āA���������ƌĂ�鎮�ό`���s���܂��B
x��2���̍���1���̍���a�ł�����ƁA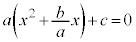 ����A
����A
�J�b�R���ɂ��āAx��1���̍��̌W��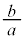 ��
��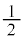 ��x�����������̂�2��̌`�����܂��B
��x�����������̂�2��̌`�����܂��B
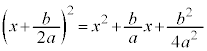
�܂�A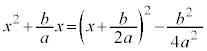 �ł��B
�ł��B
�A�ɑ������ƁA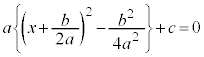
2��ȊO�̕������E�ӂɈڍ�����ƁA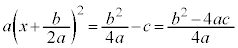
�� 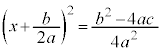
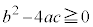 �̂Ƃ��ɂ́A(��)���g���ƁA
�̂Ƃ��ɂ́A(��)���g���ƁA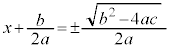
�� 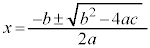
 �̂Ƃ��ɂ́A�����̉��͂���܂���B�������l����Ɖ�������܂����A���f���Q�Ƃ̂��ƁB
�̂Ƃ��ɂ́A�����̉��͂���܂���B�������l����Ɖ�������܂����A���f���Q�Ƃ̂��ƁB
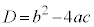 �́A2���������͎����̉��������ǂ����f����d�v�Ȏ��ł��B��������ʎ��ƌ����܂��B
�́A2���������͎����̉��������ǂ����f����d�v�Ȏ��ł��B��������ʎ��ƌ����܂��B
2���������@�́A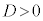 �̂Ƃ��ɁA���قȂ�2�̎������������܂��B
�̂Ƃ��ɁA���قȂ�2�̎������������܂��B
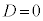 �̂Ƃ��́A1���d���F
�̂Ƃ��́A1���d���F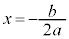 �������܂�(�������ɂ���ẮA�d������2�ƍl�����������܂�)�B
�������܂�(�������ɂ���ẮA�d������2�ƍl�����������܂�)�B
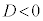 �̂Ƃ��́A�������������܂���(���قȂ�2�̋������������܂�)�B
�̂Ƃ��́A�������������܂���(���قȂ�2�̋������������܂�)�B
�Ȃ��A2���������@�ɂ����āA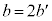 �Ə�����ꍇ�ɂ́A
�Ə�����ꍇ�ɂ́A
���́A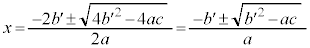 �ƂȂ�܂��B
�ƂȂ�܂��B
���̏ꍇ�ɂ́A���ʎ��́A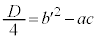 �̌`�ōl��������悢�ł��傤�B
�̌`�ōl��������悢�ł��傤�B
2���������̉�@
(1) 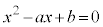 �ɂ����āA
�ɂ����āA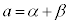 �C
�C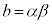 �ƂȂ�2��α�Cβ �������Ɍ�����Ȃ�A���ӂ������������āA
�ƂȂ�2��α�Cβ �������Ɍ�����Ȃ�A���ӂ������������āA
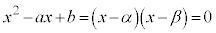 ���A���́A
���A���́A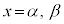
(2) 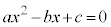 �ɂ����āA
�ɂ����āA �C
�C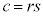 �ł����āA
�ł����āA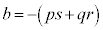 �ƂȂ�悤��4��p�Cq�Cr�Cs�������Ɍ�����Ȃ�A���ӂ������������āA
�ƂȂ�悤��4��p�Cq�Cr�Cs�������Ɍ�����Ȃ�A���ӂ������������āA
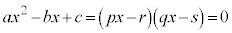 ���A���́A
���A���́A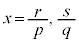
(3) 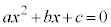 �ɂ����āA���ӂ��ȒP�Ɉ��������ł��Ȃ��Ƃ��́A���̌�����p����B
�ɂ����āA���ӂ��ȒP�Ɉ��������ł��Ȃ��Ƃ��́A���̌�����p����B
�E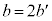 �Ə�����Ƃ��ɂ́A
�Ə�����Ƃ��ɂ́A�@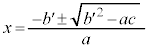 �@ �@ |
�E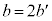 �̌`�łȂ��Ƃ��ɂ́A
�̌`�łȂ��Ƃ��ɂ́A�@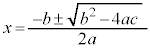 �@ �@ |
��D2���������̗�
(1) 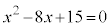
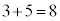 �C
�C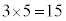 ���A���ӂ������������āA
���A���ӂ������������āA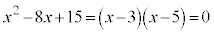
�� 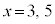
(2) 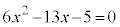
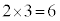 �C
�C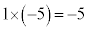 �C
�C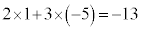 ���A���ӂ������������āA
���A���ӂ������������āA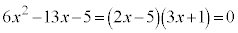
�� 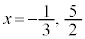
(3) 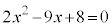
�ȒP�Ȉ��������͌�����Ȃ��̂ŁA���̌������g���B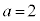 �C
�C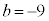 �C
�C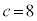 �Ƃ��āA
�Ƃ��āA
�� 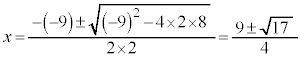
(4) 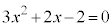
������ȒP�Ɉ��������ł��Ȃ��̂ŁA���̌������g���Bx�̌W����2�̔{���Ȃ̂ŁA
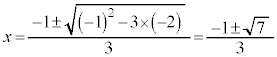
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 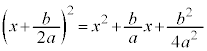
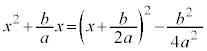 �ł��B
�ł��B