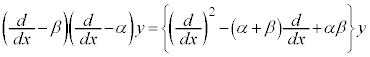微分方程式(その2) 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
微分方程式の続きです。
線形1階微分方程式と呼ばれるタイプがあります。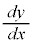 ,yの1次式で表される微分方程式です。
,yの1次式で表される微分方程式です。
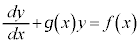 ・・・①
・・・①
という変数分離型の微分方程式を考えます。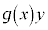 を移項して、
を移項して、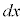 を両辺にかけyで割ることにより、
を両辺にかけyで割ることにより、
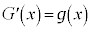 とすると、
とすると、
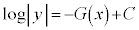 (C:積分定数)∴
(C:積分定数)∴ 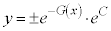
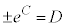 と置き直すと、
と置き直すと、
ここで①の解を考えるのですが、今定数としているDをxの関数として、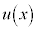 と置き直したものが①の解になると考えます。この技巧を定数変化法と言います。
と置き直したものが①の解になると考えます。この技巧を定数変化法と言います。
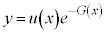 ・・・② として、
・・・② として、
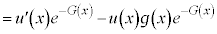
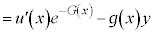 (∵ ②)
(∵ ②)
これより、
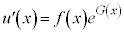 ∴
∴ 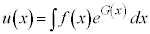
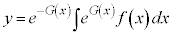 (ただし、
(ただし、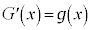 )
)
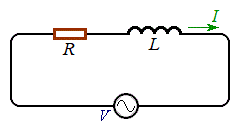 例1. 右図のような、起電力Vの交流電源と抵抗RとコイルLが直列に接続された電気回路で、起電力が
例1. 右図のような、起電力Vの交流電源と抵抗RとコイルLが直列に接続された電気回路で、起電力が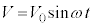 のように変化するとき、回路に流れる電流を求める。
のように変化するとき、回路に流れる電流を求める。
[解答] 電流をIとして、抵抗両端の電圧は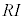 ,コイル両端の電圧は
,コイル両端の電圧は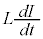
キルヒホッフの第2法則により、回路の電圧降下と起電力が等しく、
よって、
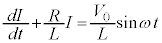 ・・・③
・・・③
(電源がない場合に相当します)を解くと、
③の解を求めるために、定数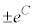 を
を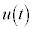 に置き換えて、
に置き換えて、
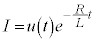 ・・・④
・・・④
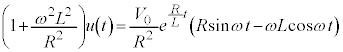 ∴
∴ 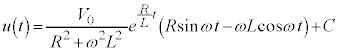 (C:積分定数)
(C:積分定数)
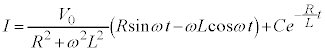 ......[答]
......[答]
物理への応用(その2)で出てきた、
のように、2階の微分、1階の微分、もとの関数の1次式で表されるタイプを線形2階微分方程式と言います。
線形2階微分方程式のうち、定数係数のものを考えます。
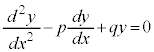 ・・・⑥
・・・⑥
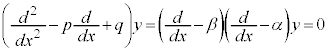 ・・・⑦
・・・⑦
となり、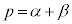 ,
,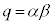 であればよいことになります。つまり、tに関する2次方程式:
であればよいことになります。つまり、tに関する2次方程式: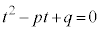 の2解をα,β として、⑦式を考えればよいのです。
の2解をα,β として、⑦式を考えればよいのです。
さて、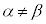 とし、⑦式を見て、
とし、⑦式を見て、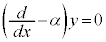 を満たす解を
を満たす解を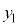 とすると、
とすると、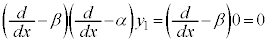 なので、
なので、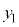 は⑦の解です。
は⑦の解です。
同様に⑦は、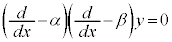 とも書けるので、
とも書けるので、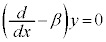 を満たす解を
を満たす解を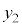 とすると、
とすると、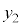 も⑦の解です。
も⑦の解です。
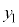 は
は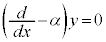 を満たすので、
を満たすので、
同様に、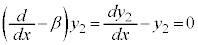 の解は、
の解は、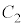 を定数として、
を定数として、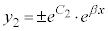
ここで、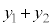 という関数を考えると、
という関数を考えると、
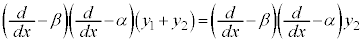
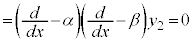
となり、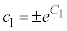 ,
,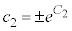 として、
として、
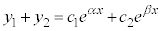 ・・・⑧
・・・⑧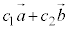 にならって一次結合と言います)は⑦の解になっています。
にならって一次結合と言います)は⑦の解になっています。
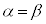 の場合には、⑦は、
の場合には、⑦は、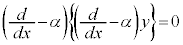 となりますが、中カッコの中をzとすると、
となりますが、中カッコの中をzとすると、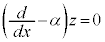 の解はcを定数として、
の解はcを定数として、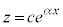
よって、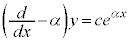 の解を、線形1階微分方程式で用いた定数変化法を用いて、
の解を、線形1階微分方程式で用いた定数変化法を用いて、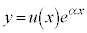 として代入すると、
として代入すると、
⑦が、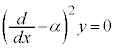 となったときの解は、
となったときの解は、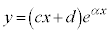 となります。
となります。
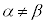 の場合に戻ります。
の場合に戻ります。
2次方程式: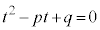 が、判別式:
が、判別式: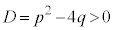 であって、α,β がともに実数の場合には,⑧で問題ありませんが、
であって、α,β がともに実数の場合には,⑧で問題ありませんが、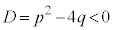 であって、α,β が虚数の場合には、
であって、α,β が虚数の場合には、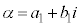 ,
,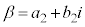 (iは虚数単位)だとして、⑦の解が、
(iは虚数単位)だとして、⑦の解が、
ということになってしまいます。このときには、オイラーの公式: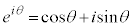 を用い、
を用い、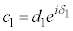 ,
,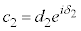 として、
として、
yが実数であるなら、
となります。
p,qが実数であるときには、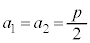 ,
,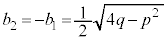 となり、
となり、
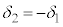 となるように、
となるように、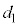 ,
,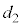 を決めておけば、
を決めておけば、
この場合には、解を、
の形に書くことができます(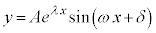 の形でもよい)。
の形でもよい)。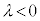 の場合には、減衰振動(物理への応用(その2)を参照)を表します。
の場合には、減衰振動(物理への応用(その2)を参照)を表します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
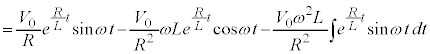
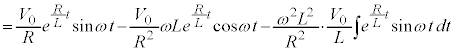
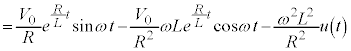 (∵ ⑤)
(∵ ⑤)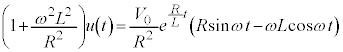
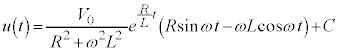 (C:積分定数)
(C:積分定数)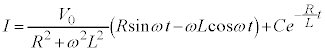 ......[答]
......[答]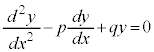 ・・・⑥
・・・⑥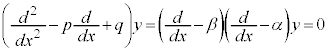 ・・・⑦
・・・⑦