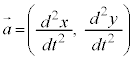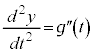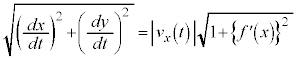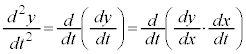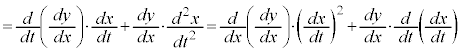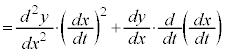�����ւ̉��p
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(1) 1�����̉^���F����t�ɂ����镨�̂̈ʒu��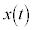 ���Ƃ��āA
���Ƃ��āA ���̂̑��x�́A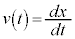
���̂̑����́A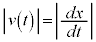
���̂̉����x�́A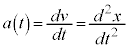
����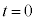 �ɂ�����A���̂̈ʒu��
�ɂ�����A���̂̈ʒu��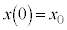 �C���x��
�C���x��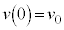 ���Ƃ��āA����t�ɂ���������x
���Ƃ��āA����t�ɂ���������x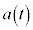 ���^�����Ă���Ƃ��A
���^�����Ă���Ƃ��A ����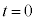 ���玞��t�̊ԂɁA���̂����������̂�́A
���玞��t�̊ԂɁA���̂����������̂�́A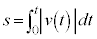
(2) 2�����̉^���F����t�ɂ����镨�̂̈ʒu��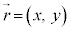 ���Ƃ��āA
���Ƃ��āA ���̂̑��x�́A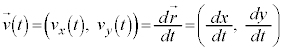
���̂̑����́A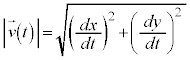
���̂̉����x�́A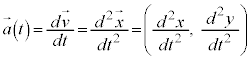
����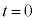 �ɂ�����A���̂̈ʒu��
�ɂ�����A���̂̈ʒu��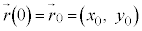 �C���x��
�C���x��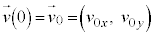 ���Ƃ��āA����t�ɂ���������x
���Ƃ��āA����t�ɂ���������x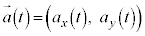 ���^�����Ă���Ƃ��A
���^�����Ă���Ƃ��A
��L�ł́A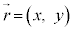 �Ƃ��āA�x�N�g��
�Ƃ��āA�x�N�g��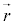 �̔���
�̔���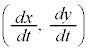 ���A
���A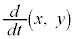 �̂悤�Ɍ��āA
�̂悤�Ɍ��āA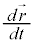 �Ə����Ă��܂��B
�Ə����Ă��܂��B
�܂��A�x�N�g��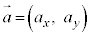 �̐ϕ�
�̐ϕ�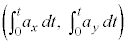 ���A
���A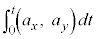 �̂悤�Ɍ��āA
�̂悤�Ɍ��āA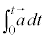 �Ə����Ă��܂��B
�Ə����Ă��܂��B
��������^�����镨�̂��A����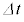 �̊Ԃ�
�̊Ԃ�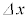 �������W���ω�����Ƃ��A
�������W���ω�����Ƃ��A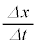 �ϑ��x�ƌ����܂��B
�ϑ��x�ƌ����܂��B
x�����Ԃ̊��ł���Ȃ�A���ϑ��x�́A��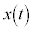 �̕��ϕω����ɑ������܂��B
�̕��ϕω����ɑ������܂��B
���ϑ��x�ŁA����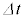 �̊Ԃɂǂꂾ���i�ނ��Ƃ������Ƃ��r���邱�Ƃ��ł��܂����A���ϑ��x���̂����X���X�ω����Ă���悤�ȏꍇ�ɂ́A���ϑ��x�ł͕��̂̈ړ����������x������r���邱�Ƃ��ł��Ȃ��Ƃ�������܂��B
�̊Ԃɂǂꂾ���i�ނ��Ƃ������Ƃ��r���邱�Ƃ��ł��܂����A���ϑ��x���̂����X���X�ω����Ă���悤�ȏꍇ�ɂ́A���ϑ��x�ł͕��̂̈ړ����������x������r���邱�Ƃ��ł��Ȃ��Ƃ�������܂��B
�e�u�Ԃɂ�����ړ����������x������]�����邽�߂ɁA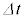 ���ɂ߂ĒZ���Ƃ邱�Ƃ��l���܂��B���w��ł́A
���ɂ߂ĒZ���Ƃ邱�Ƃ��l���܂��B���w��ł́A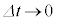 �Ƃ����Ƃ��̋Ɍ����l���邱�ƂɂȂ�܂��B
�Ƃ����Ƃ��̋Ɍ����l���邱�ƂɂȂ�܂��B
 �̂̑��x�ƌ����܂��B�����A
�̂̑��x�ƌ����܂��B�����A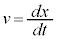 �ł��B
�ł��B
���l�ɁA���x�ω��̓x������]�����邽�߂ɁA����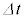 �̊Ԃ̑��x�ω���
�̊Ԃ̑��x�ω���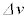 �Ƃ��āA
�Ƃ��āA
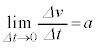 �̂̉����x�ƌ����܂��A�����A
�̂̉����x�ƌ����܂��A�����A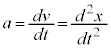 �ł��B
�ł��B
�܂��A���x�̐�Βl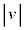 �𑬂��ƌ����܂��B
�𑬂��ƌ����܂��B
����t�̊��Ƃ��ĉ����x��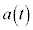 �Ɨ^�����Ă���Ƃ��A
�Ɨ^�����Ă���Ƃ��A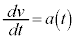 ���A
���A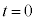 �ɂ����鑬�x��
�ɂ����鑬�x��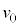 �Ƃ��āA
�Ƃ��āA
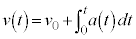 �@(���ӂ��������Ίm���߂��܂�)�@����@
�@(���ӂ��������Ίm���߂��܂�)�@����@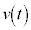 �Ɨ^�����Ă���Ƃ��A
�Ɨ^�����Ă���Ƃ��A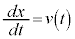 ���A
���A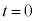 �ɂ����镨�̂̍��W��
�ɂ����镨�̂̍��W��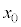 �Ƃ��āA
�Ƃ��āA
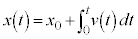 �@(���ӂ��������Ίm���߂��܂�)�@����A
�@(���ӂ��������Ίm���߂��܂�)�@����A
(i) �ꎟ���������x�^��
��������^�����镨�̂̉����xa�����ł���^�������x�^���ƌ����܂��B
����t�ɂ����鑬�x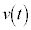 �́A
�́A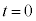 �ɂ����鑬�x��
�ɂ����鑬�x��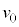 �Ƃ���ƁA�@�ɂ��A
�Ƃ���ƁA�@�ɂ��A
����t�ɂ����镨�̂̍��W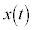 �́A
�́A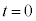 �ɂ�������W��
�ɂ�������W��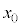 �Ƃ��āA�A�ɂ��A
�Ƃ��āA�A�ɂ��A
(ii) ���̉^��
���A�O�����̉^���ł́A���̂̈ʒu�A���x�A�����x��\���̂Ƀx�N�g����p���܂��B
���̉^���A�܂�A���̂����ʏ���^������Ƃ��́A���̂̈ʒu�̍��W��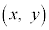 �Ƃ��āAx�����̉^���Ay�����̉^���A���ꂼ����ꎟ���̉^���̂悤�ɍl���܂��B���̂̈ʒu�́A
�Ƃ��āAx�����̉^���Ay�����̉^���A���ꂼ����ꎟ���̉^���̂悤�ɍl���܂��B���̂̈ʒu�́A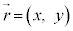 �C���̂̑��x�́A
�C���̂̑��x�́A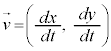 �C���̂̉����x�́A
�C���̂̉����x�́A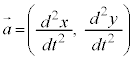
�܂�A���x��x������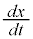 �C���x��y������
�C���x��y������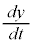 �ł��B�����x��x������
�ł��B�����x��x������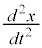 �C�����x��y������
�C�����x��y������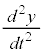 �ł��B
�ł��B
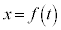 �C
�C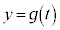 �̂悤�ɗ^�����Ă���ꍇ�A
�̂悤�ɗ^�����Ă���ꍇ�A
���x��x�����́A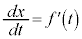
���x��y�����́A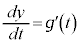
�����x��x�����́A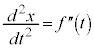
�����x��y�����́A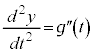
���̂̉^���o�H�������Ȑ��̎��F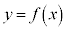 �ƁA���x��x�����F
�ƁA���x��x�����F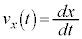 ���^�����Ă���ꍇ�A
���^�����Ă���ꍇ�A
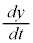 �����߂�̂ɂ́A�������̔����@�𗘗p���܂��B
�����߂�̂ɂ́A�������̔����@�𗘗p���܂��B
���x��y�����́A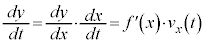
�����́A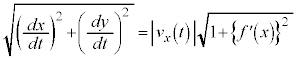
�����x��x�����́A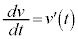
�����x��y�����́A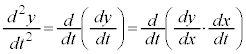
���ʏ�̒����ɉ����āA�������x�^�����镨�̂̉����x��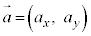 �Ɨ^�����Ă���(
�Ɨ^�����Ă���(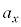 �C
�C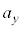 �͒萔)�Ƃ��A
�͒萔)�Ƃ��A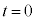 �ɂ����鑬�x��
�ɂ����鑬�x��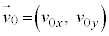 �C����t�ɂ����鑬�x��
�C����t�ɂ����鑬�x��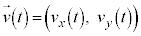 �Ƃ��āA�@�ɂ��A
�Ƃ��āA�@�ɂ��A
����2����1�ɂ܂Ƃ߂āA�ȉ��̂悤�ɏ������Ƃɂ��܂��B
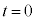 �ɂ����镨�̂̈ʒu�x�N�g����
�ɂ����镨�̂̈ʒu�x�N�g����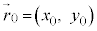 �C����t�ɂ����镨�̂̈ʒu�x�N�g����
�C����t�ɂ����镨�̂̈ʒu�x�N�g����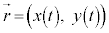 �Ƃ��āA�A�ɂ��A
�Ƃ��āA�A�ɂ��A
����2����1�ɂ܂Ƃ߂āA�ȉ��̂悤�ɏ������Ƃɂ��܂��B
���ʏ�̉~���ɉ����āA���̑����œ������̂̉^�����~�^���ƌ����܂��B���̂̈ʒu���w���ʒu�x�N�g����x���Ƃ̂Ȃ��pθ �́A����t��1�����Ƃ��āA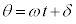 �ƕ\�����Ƃ��ł��܂��Bω ���p���x�Aδ�������ʑ��ƌ����܂��B
�ƕ\�����Ƃ��ł��܂��Bω ���p���x�Aδ�������ʑ��ƌ����܂��B
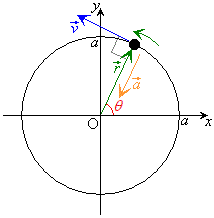 ������A���aA�̉~���ɉ����Ĕ����v���(
������A���aA�̉~���ɉ����Ĕ����v���(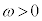 )�ɓ����~�^�����镨�̂̈ʒu�x�N�g���́A
)�ɓ����~�^�����镨�̂̈ʒu�x�N�g���́A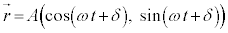
���x�x�N�g���́A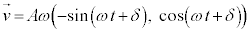
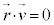 ���A���̂̑��x�͓��a�Ɛ����ɂȂ��Ă��邱�Ƃ��킩��܂��B
���A���̂̑��x�͓��a�Ɛ����ɂȂ��Ă��邱�Ƃ��킩��܂��B
�܂��A���̂̑����́A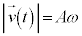
�����x�x�N�g���́A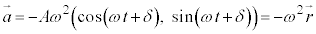
�ƂȂ�A�ʒu�x�N�g���Ƃ��傤�Njt�����ŁA���̂̈ʒu����~�̒��S�Ɍ������Ă��邱�Ƃ��킩��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 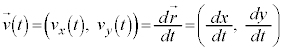
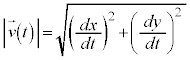
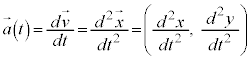
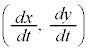 ���A
���A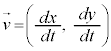 �C���̂̉����x�́A
�C���̂̉����x�́A