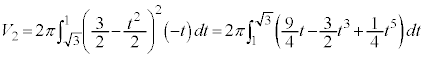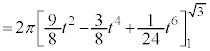y���̉��̉�]���@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�s��ϕ��̌����A��ϕ��Ƒ̐����Q�Ƃ��Ă��������B
�Ȑ��F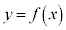 �ƒ����F
�ƒ����F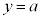 �C�����F
�C�����F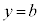 (
(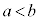 �Ƃ���)�C�y��y���ň͂܂��}�`��y���̉���1��]�����Ăł����]�̂̑̐�V�́A
�Ƃ���)�C�y��y���ň͂܂��}�`��y���̉���1��]�����Ăł����]�̂̑̐�V�́A
��]�̂�y���ɐ����ȕ��ʁF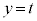 �Ő����Ƃ��̒f�ʂ́A
�Ő����Ƃ��̒f�ʂ́A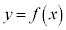 �̋t��
�̋t��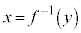 �𗘗p���ď����ƁA���a
�𗘗p���ď����ƁA���a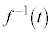 �̉~�Ȃ̂ŁA
�̉~�Ȃ̂ŁA
�f�ʐρF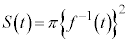
����āA��]�̂̑̐�V�́A
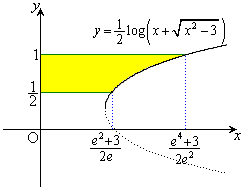 ��1�D�@�Ȑ��F
��1�D�@�Ȑ��F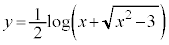 �ƒ���
�ƒ���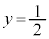 �C����
�C����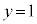 �ň͂܂ꂽ�}�`��y���̂܂���1��]�����Ăł����]�̂̑̐ς����߂�B
�ň͂܂ꂽ�}�`��y���̂܂���1��]�����Ăł����]�̂̑̐ς����߂�B
[��]�@�܂��A�Ȑ��̕�������x�ɂ��ĉ����K�v������܂��B
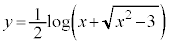 ��
�� 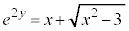 �@����@
�@����@
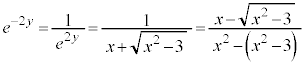 �@(�����L��������)
�@(�����L��������)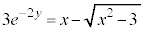 �@����A
�@����A
�@�{�A���A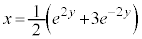
���A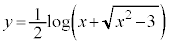 �͒P�������ł��B
�͒P�������ł��B
�]���āA���߂��]�̂̑̐�V�́A
��1�D�̂悤�ɁA�t�������邱�Ƃ̂ł�����̏ꍇ�ɂ́Ay���̂܂��̉�]�̂͏�L�̌����Ōv�Z�ł���̂ł����A�t�������߂邱�Ƃ��ł��Ȃ��ꍇ�ɂ́A�ʂ̕��@���l���܂��B
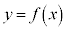 �̋t��
�̋t��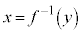 �����߂��Ȃ����A���ɐϕ����Â炢�`�ɂȂ�Ƃ��܂��B
�����߂��Ȃ����A���ɐϕ����Â炢�`�ɂȂ�Ƃ��܂��B
�Ȑ��F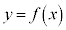 �ƁA����
�ƁA����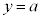 �C����
�C����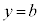 �ň͂܂ꂽ�}�`��y���̂܂���1��]�������Ƃ��̑̐�V�́A
�ň͂܂ꂽ�}�`��y���̂܂���1��]�������Ƃ��̑̐�V�́A
�ł����Ax��y�ŕ\���Ȃ����A�\���Ă��ϕ����Â炢�Ƃ��́A�ȉ��̂悤�ɁA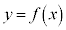 �Ƃ����āA�u���ϕ����܂��B
�Ƃ����āA�u���ϕ����܂��B
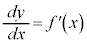 ���A
���A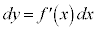 �Cy�F
�Cy�F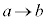 �̂Ƃ��Ax�F
�̂Ƃ��Ax�F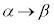 �Ƃ����(
�Ƃ����(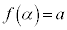 �C
�C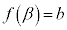 )�A
)�A
���̌`�̂܂܌v�Z�ł��Ă��܂����̂́A�ϕ��v�Z�����s���܂��B
�ł����A���̌`�ł��A�ϕ��̌v�Z�����ɂ����ꍇ�ɂ́A�����ϕ����āA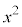 ������A
������A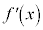 ��ϕ��ɉāA
��ϕ��ɉāA
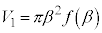 �́A��~�̔��a��β�C������
�́A��~�̔��a��β�C������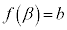 �̉~���̑̐ςł��B
�̉~���̑̐ςł��B
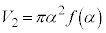 �́A��~�̔��a��α�C������
�́A��~�̔��a��α�C������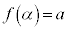 �̉~���̑̐ςł��B
�̉~���̑̐ςł��B
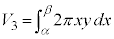 �́A��~�̔��ax (��~�̉~���̒�����
�́A��~�̔��ax (��~�̉~���̒�����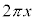 )�C����y�̉~�����J���Ē����`�ɂ����Ƃ��̒����`�̖ʐρF
)�C����y�̉~�����J���Ē����`�ɂ����Ƃ��̒����`�̖ʐρF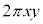 ��x�����ɐϕ��������̂ŁA�Ȑ��F
��x�����ɐϕ��������̂ŁA�Ȑ��F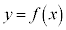 �ƒ���
�ƒ���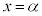 �C����
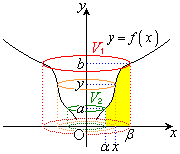
�C����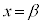 �Cx���ň͂܂�镔��(�E�}�ʼn��F�ɓh��ꂽ����)��y���̂܂���1��]���Ăł����]�̂̑̐ς�\���Ă��܂��B
�Cx���ň͂܂�镔��(�E�}�ʼn��F�ɓh��ꂽ����)��y���̂܂���1��]���Ăł����]�̂̑̐ς�\���Ă��܂��B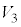 �̑̐ς̍l�����́A��]�̂��~���ɕ������đ̐ς��v�Z����Ƃ����Ӗ��ŁA�~�������ƌĂ�Ă��܂��B
�̑̐ς̍l�����́A��]�̂��~���ɕ������đ̐ς��v�Z����Ƃ����Ӗ��ŁA�~�������ƌĂ�Ă��܂��B
����y���̂܂��̉�]�̂̑̐ς́A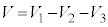 �ɂȂ��Ă��܂��B
�ɂȂ��Ă��܂��B
�ȉ��ɁA�~�������ł��܂��Ay���̂܂��̉�]�̂̑̐ς��v�Z�ł�����2�����Ă����܂��B
��2�D�@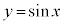 ��
��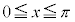 �̕�����x���ň͂܂��}�`��y���̂܂���1��]���Ăł����]�̂̑̐ς����߂�B
�̕�����x���ň͂܂��}�`��y���̂܂���1��]���Ăł����]�̂̑̐ς����߂�B
[��]�@���߂�̐ς�V�Ƃ���ƁA��̉~�������̍l�����ɂ��A
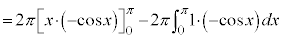
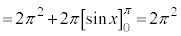 ......[��]
......[��]
��3�D�@�Ȑ��F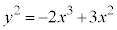 ��
��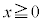 �̕����Cx���Cy���C
�̕����Cx���Cy���C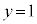 �ň͂܂��}�`��y���̂܂���1��]���Ăł����]�̂̑̐ς����߂�B
�ň͂܂��}�`��y���̂܂���1��]���Ăł����]�̂̑̐ς����߂�B
[��]�@���߂�̐ς�V�Ƃ��܂��B
�Ȑ��̎���x�ɂ��ĉ������Ƃ��Ă��A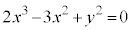 �ł͑�ςȂ��ƂɂȂ�܂��B
�ł͑�ςȂ��ƂɂȂ�܂��B
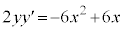 ���
���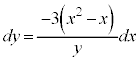 �ƂȂ�̂ŁA�u���ϕ������������ł��B�����ŁA�~���������l���܂��B
�ƂȂ�̂ŁA�u���ϕ������������ł��B�����ŁA�~���������l���܂��B
���߂�̐�V�́A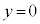 �̂Ƃ�
�̂Ƃ�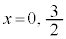 �C
�C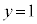 �̂Ƃ�
�̂Ƃ�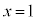 �Ȃ̂ŁA��~�̔��a1�C����1�̉~���̑̐�
�Ȃ̂ŁA��~�̔��a1�C����1�̉~���̑̐�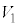 ����A�Ȑ��F
����A�Ȑ��F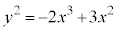 ��x���A����
��x���A����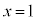 �ň͂܂�镔����y���̉���1��]���Ăł����]�̂̑̐�
�ň͂܂�镔����y���̉���1��]���Ăł����]�̂̑̐�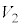 �����������̂ɂȂ�܂��B
�����������̂ɂȂ�܂��B
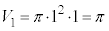
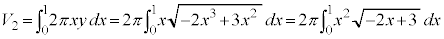
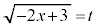 �Ƃ����ƁA
�Ƃ����ƁA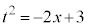 �C
�C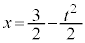 �C��������
�C��������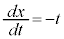 ���A
���A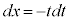 �Cx�F
�Cx�F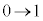 �̂Ƃ��At�F
�̂Ƃ��At�F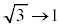
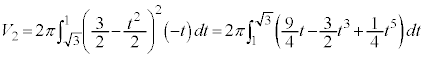
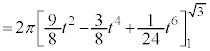
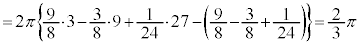 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 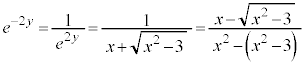 �@(�����L��������)
�@(�����L��������)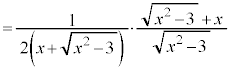
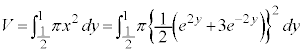
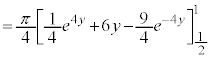
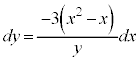 �ƂȂ�̂ŁA�u���ϕ������������ł��B�����ŁA�~���������l���܂��B
�ƂȂ�̂ŁA�u���ϕ������������ł��B�����ŁA�~���������l���܂��B