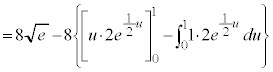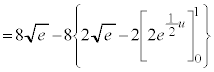定積分と体積 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、不定積分の公式を参照してください。
座標空間中の、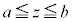 の範囲に置かれた立体図形をxy平面に平行な平面
の範囲に置かれた立体図形をxy平面に平行な平面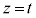 で切断したときの断面積を
で切断したときの断面積を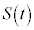 とすると、この立体図形の体積Vは、
とすると、この立体図形の体積Vは、
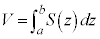
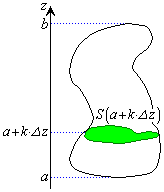
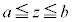 の範囲をn等分し、
の範囲をn等分し、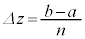 ,
,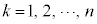 として、平面
として、平面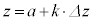 で立体図形を切断したときの断面積は
で立体図形を切断したときの断面積は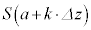 です。このときの切断面を底面とし、高さ
です。このときの切断面を底面とし、高さ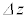 の柱体
の柱体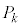 を考えると、
を考えると、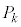 の体積は、
の体積は、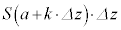 で与えられます。
で与えられます。
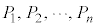 の体積の総和:
の体積の総和: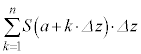 は、
は、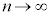 の極限で立体の体積Vに近づきます。よって、区分求積法により、
の極限で立体の体積Vに近づきます。よって、区分求積法により、
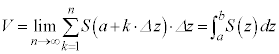
例1. 半径rの円を底面とし、高さhの円錐の体積を求める。
[解答] 底面の円がxy平面上に置かれているとして考えます。
平面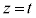 (
(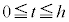 )で円錐を切ったときの断面の円の半径を
)で円錐を切ったときの断面の円の半径を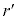 として、r:
として、r: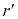 = h:
= h: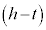
∴ 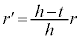
断面の円の面積は、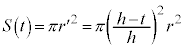
よって、円錐の体積は、
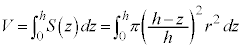
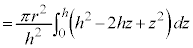
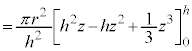
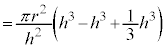
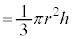 ......[答]
......[答]
円錐に限らず、底面積S,高さhの錐体では、平面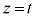 で切断したときの断面積が
で切断したときの断面積が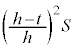 で与えられるので、上記と同じように積分して、錐体の体積Vは、
で与えられるので、上記と同じように積分して、錐体の体積Vは、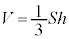 となります。
となります。
例2. 半径rの球の体積を求める。
[解答] 球の中心が原点にあるとして考えます。
平面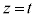 (
(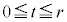 )で球を切ったときの断面の円の半径を
)で球を切ったときの断面の円の半径を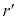 として、三平方の定理より、
として、三平方の定理より、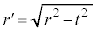
断面の円の面積は、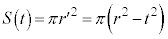
よって、球の体積Vは、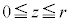 の部分にある半球の体積の2倍として、
の部分にある半球の体積の2倍として、
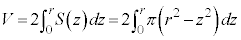
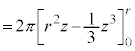
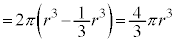 ......[答]
......[答]
例3. tが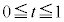 の範囲を動くとき、zx平面上の曲線:
の範囲を動くとき、zx平面上の曲線: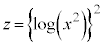 (
(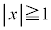 ),および、yz平面上の曲線
),および、yz平面上の曲線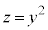 と、平面
と、平面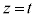 との4交点を頂点とする四角形の外周及びその内部の領域が通過する部分の体積を求める。
との4交点を頂点とする四角形の外周及びその内部の領域が通過する部分の体積を求める。
[解答] 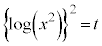 とすると、
とすると、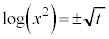
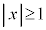 より、
より、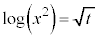 ,
,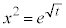 ,
,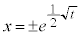
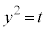 とすると、
とすると、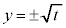
よって、体積を求める部分の立体を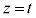 で切った断面の四角形の面積は、
で切った断面の四角形の面積は、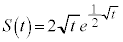
求める体積Vは、
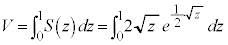
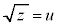 とおく(置換積分を参照)と、
とおく(置換積分を参照)と、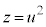 ,
,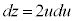 ,z:
,z: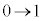 のとき、u:
のとき、u: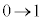
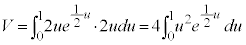
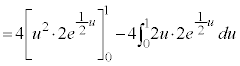 (部分積分法を参照)
(部分積分法を参照)
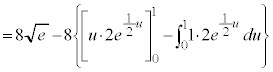
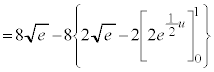
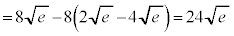 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 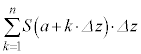 は、
は、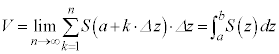
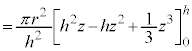
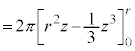
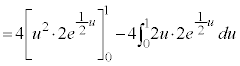 (部分積分法を参照)
(部分積分法を参照)