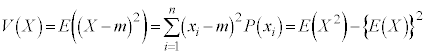確率分布 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
サイコロを振ったとき、4が出たら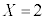 ,2か6が出たら
,2か6が出たら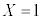 ,1か3か5が出たら
,1か3か5が出たら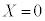 だとします。
だとします。
1回サイコロを振って、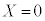 になる確率は
になる確率は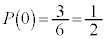 ,
,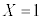 になる確率は
になる確率は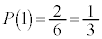 ,
,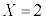 になる確率は
になる確率は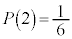 です。この状況を表にして表すと、
です。この状況を表にして表すと、
このように、Xがとりうる値xに対して確率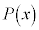 が決まる関係を、確率分布と言います。また、Xを確率変数と言います。
が決まる関係を、確率分布と言います。また、Xを確率変数と言います。
一般的に、n個の要素をもつ集合Uの要素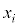 (
(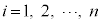 )について、
)について、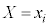 のとき、確率
のとき、確率 が定まり、
が定まり、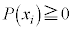 かつ
かつ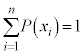 であるときに、Xを確率変数と言い、Xがとりうる値
であるときに、Xを確率変数と言い、Xがとりうる値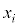 に対して確率
に対して確率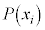 が以下の表(*)のように決まる関係を確率分布と言います。
が以下の表(*)のように決まる関係を確率分布と言います。
このとき、確率変数Xは、上記の表(*)で定まる確率分布に従う、という言い方をします。
また、以上のように集合Uの要素が有限個か、あるいは、仮に無限個あったとしても集合Uが1個、2個、3個、・・・と数えていけるようなものである場合には、確率変数を特に離散型確率変数、確率分布を離散型確率分布と言います。
確率変数Xが表(*)で定まる確率分布に従うとき、
をXの平均または期待値と言います。
最初に出てきた確率分布、
においては、Xの期待値は、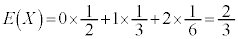 となります。
となります。
集合Uの要素の個数を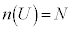 ,Uの部分集合
,Uの部分集合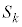 (
(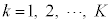 )について、すべての部分集合の相異なるどの2個
)について、すべての部分集合の相異なるどの2個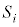 ,
,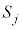 (
(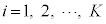 ,
,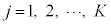 ,
,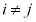 )についても
)についても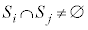 かつ
かつ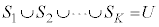 であるとき、集合
であるとき、集合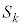 の個数を
の個数を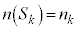 とすると、
とすると、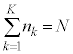 です。
です。
集合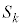 のすべての要素について、確率変数Xが
のすべての要素について、確率変数Xが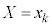 という値をとるとします。集合Uのすべての要素について同様に確からしいとすると、確率変数Xが
という値をとるとします。集合Uのすべての要素について同様に確からしいとすると、確率変数Xが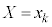 という値をとる確率
という値をとる確率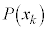 は
は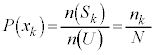 です。このとき、確率変数Xの平均
です。このとき、確率変数Xの平均
は、Uの全要素がとる値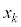 の平均値、つまりXの平均値
の平均値、つまりXの平均値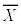 です。
です。
再び、n個の要素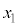 ,
,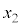 ,・・・,
,・・・,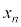 からなる集合Uのもとで、確率変数Xが
からなる集合Uのもとで、確率変数Xが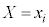 という値をとる確率を
という値をとる確率を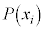 とする確率分布を考えます。平均と同様に、
とする確率分布を考えます。平均と同様に、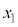 ,
,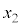 ,・・・,
,・・・,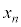 のデータの散らばりの程度を表す量、即ちXの分散
のデータの散らばりの程度を表す量、即ちXの分散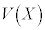 を、
を、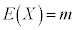 として、
として、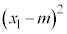 ,
,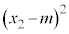 ,・・・,
,・・・,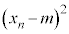 という値をとる確率変数
という値をとる確率変数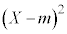 の平均(期待値)と考えて、
の平均(期待値)と考えて、
として定義します。また、Xの標準偏差は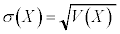 です。確率分布における分散についても、
です。確率分布における分散についても、
ここで、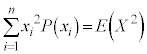 ,
,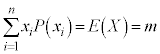 ,
,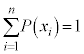 より、
より、
となります。つまり、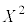 の平均からXの平均の2乗を引くことによりXの分散を求めることができます。
の平均からXの平均の2乗を引くことによりXの分散を求めることができます。
確率変数Xが、表(*)で表される確率分布に従うとします。このとき、a,bを定数として、 によって、新たな確率変数Yを考え、
によって、新たな確率変数Yを考え、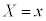 のとき、
のとき、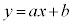 として確率変数Yが
として確率変数Yが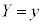 となるとき、このXとYの対応関係を、Xに対する確率変数の変換と言います。
となるとき、このXとYの対応関係を、Xに対する確率変数の変換と言います。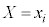 (
(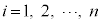 )のとき、
)のとき、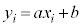 として、
として、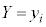 となりますが、
となりますが、 となる確率
となる確率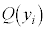 は、
は、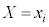 となる確率に等しく、
となる確率に等しく、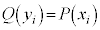 です。このとき、Yの平均
です。このとき、Yの平均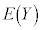 と分散
と分散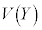 は、
は、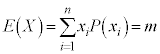 ,
,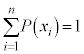 ,
,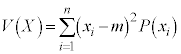 より、
より、
標準偏差については、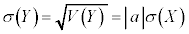
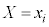 (
(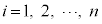 )に対して、以下の性質を満たす確率
)に対して、以下の性質を満たす確率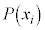 が定まるとき、この関係を確率分布、Xを確率変数と言う。
が定まるとき、この関係を確率分布、Xを確率変数と言う。
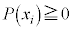 ,
,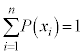
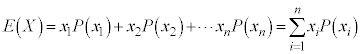 (
(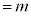 とする)
とする)
確率変数Xの分散: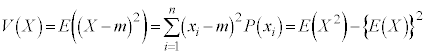
確率変数Xの標準偏差: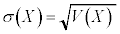
確率変数の変換: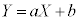 (a,bは定数)に対して、
(a,bは定数)に対して、
確率変数Yの平均: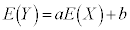
確率変数Yの分散: ,確率変数Yの標準偏差:
,確率変数Yの標準偏差: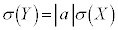
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 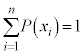 であるときに、Xを確率変数と言い、Xがとりうる値
であるときに、Xを確率変数と言い、Xがとりうる値
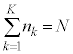 です。
です。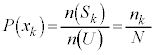 です。このとき、確率変数Xの平均
です。このとき、確率変数Xの平均
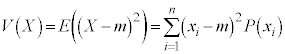
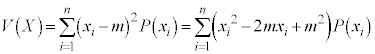
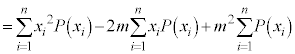
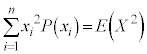 ,
,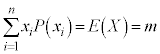 ,
,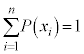 より、
より、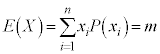 ,
,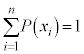 ,
,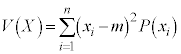 より、
より、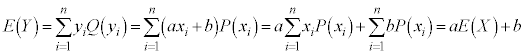
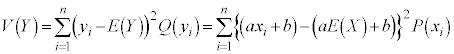
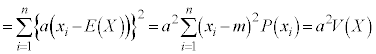
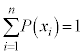
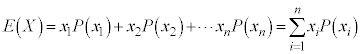 (
(