確率 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
サイコロを振ると、1か2か3か4か5か6の目が出ます。それぞれの目が出る割合は何度振っても変わりません。このように同じ割合で、ある結果が起こることが期待される実験を試行と言います。
試行の結果起こるできごとを事象と言います。
1の目が出る事象、2の目が出る事象、・・・、6の目が出る事象、すべて合わせて、全事象と言います。
1の目が出る事象、2の目が出る事象、など、1つ1つの事象を全事象に対して、根元事象と言います。
サイコロを振るという試行に対して、各事象を出る目の数で表すことにすると、全事象を全体集合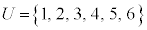 として考えることができます。事象は全体集合の部分集合、根元事象は全体集合の要素の1つだけを持つ集合
として考えることができます。事象は全体集合の部分集合、根元事象は全体集合の要素の1つだけを持つ集合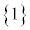 ,
,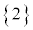 ,・・・,
,・・・,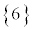 と考えることができます。
と考えることができます。
空集合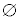 に対する事象を空事象と言います。
に対する事象を空事象と言います。
サイコロを振るという試行では、1から6までの目の出る割合は同じです。6万回振れば、1から6までの目はほぼ1万回ずつ出ます。
このようなときに、これらの根元事象は「同様に確からしい」、という言い方をします。
このときに、事象Eの場合の数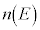 を全事象の場合の数
を全事象の場合の数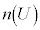 で割ったもの
で割ったもの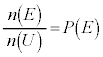 を、事象Eの起こる確率と言います。
を、事象Eの起こる確率と言います。
確率は、事象Eの起こりやすさを表す数値です。
3の目が出るという事象を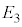 と書くと、
と書くと、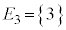 ,3の目が出る確率
,3の目が出る確率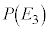 は、
は、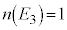 ,
,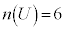 より、
より、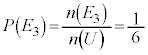 です。
です。
偶数の目が出るという事象を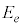 と書くと、
と書くと、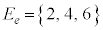 ,偶数の目が出る確率
,偶数の目が出る確率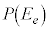 は、
は、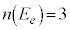 より、
より、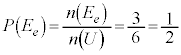 です。
です。
3の倍数の目が出るという事象を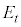 と書くと、
と書くと、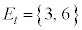 ,3の倍数の目が出る確率
,3の倍数の目が出る確率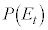 は、
は、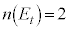 より、.
より、. .です。
.です。
根元事象や、全事象は、問題によっていろいろなとらえ方をすることができます。
サイコロを振る場合、出た目を3で割った余り0,1,2を考えて、全事象を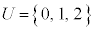 とし、出た目が3の倍数であるという事象を
とし、出た目が3の倍数であるという事象を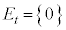 として、3の倍数の目が出る確率を
として、3の倍数の目が出る確率を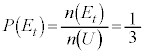 というように考えることもできます。ただし、ここで考えている3つの根元事象
というように考えることもできます。ただし、ここで考えている3つの根元事象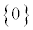 ,
,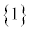 ,
,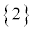 は、同様に確からしくなければなりません。
は、同様に確からしくなければなりません。
サイコロを振って、出た目を4で割った余り0,1,2,3を考えると、事象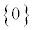 と事象
と事象 とは同様に確からしくはありません。
とは同様に確からしくはありません。
サイコロを2回振って出た目の和は、1と1の和の2から6と6の12まで11通りの可能性がありますが、根元事象を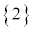 ,
,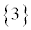 ,・・・,
,・・・,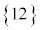 ,また、全事象を
,また、全事象を と考えることはできません。サイコロを2回振って出た目の和が4になる確率を
と考えることはできません。サイコロを2回振って出た目の和が4になる確率を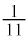 とするのは誤りです。なぜなら、根元事象
とするのは誤りです。なぜなら、根元事象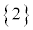 ,
,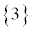 ,・・・,
,・・・,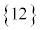 は、「同様に確からしい」と言えないからです。
は、「同様に確からしい」と言えないからです。
サイコロを2回振って出た目のパターンは、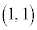 ,
,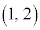 ,・・・,
,・・・,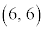 の36パターンあります。この36パターンの各一は同様に確からしいと言えるので、根元事象を
の36パターンあります。この36パターンの各一は同様に確からしいと言えるので、根元事象を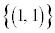 ,
,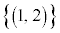 ,・・・,
,・・・,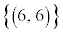 とし、全事象を
とし、全事象を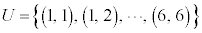 と考えることができます。このとき、出た目の和が4になるという事象は、
と考えることができます。このとき、出た目の和が4になるという事象は、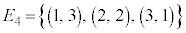 です。従って、サイコロを2回振って出た目の和が4になる確率は、
です。従って、サイコロを2回振って出た目の和が4になる確率は、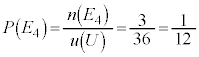 となります。
となります。
根元事象を「同様に確からしい」と言えるように考えているか、という点が、確率の問題で最も間違いやすい点なので、よく注意してください。
同種のサイコロを2個振って出た目の和が4になる確率も、サイコロを2回振って出た目の和が4になる確率と全く同様に考えます。
サイコロに区別がないのだから、どちらが1でどちらが3なのか区別ができないではないか、というように疑問を持つ人もいると思いますが、確率の問題では、根元事象を「同様に確からしい」ものとして考える必要があります。「1の目と3の目が出る」という事象と「2の目が2個出る」という事象とでは、起こりやすさが倍違うのです。従って、同種のサイコロを2個振る場合でも、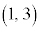 と
と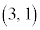 を区別して、根元事象を、
を区別して、根元事象を、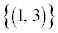 ,
,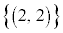 ,
,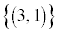 というように考えなければなりません。確率の問題では、問題文に「同じサイコロを2個」とか「同じ球を3個」というように書かれていても、2個のサイコロを異なるサイコロとして区別し、同じ球3個を異なる球として区別して考えるべきです。簡単なことのように感じるかも知れませんが、重要なポイントです。
というように考えなければなりません。確率の問題では、問題文に「同じサイコロを2個」とか「同じ球を3個」というように書かれていても、2個のサイコロを異なるサイコロとして区別し、同じ球3個を異なる球として区別して考えるべきです。簡単なことのように感じるかも知れませんが、重要なポイントです。
例.10個の同種の球を袋A,袋B,袋Cにでたらめに入れていくとき、袋Aに3個、袋Bに2個入る確率を求めよ。
[解答] 袋Aに3個、袋Bに2個入れば、自動的に袋Cに5個入るので、全事象の場合の数を、3種類のものから重複を許して10個とる重複組み合わせの数と考えて、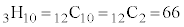 通りとし、求める確率を
通りとし、求める確率を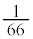 とするのは誤りです。
とするのは誤りです。
なぜなら、ここで考えている全事象の66通りの各1通りは、「同様に確からしい」とは言えないからです。
「袋Aに3個、袋Bに2個、袋Cに5個入る」事象Dと、「袋Aに4個、袋Bに2個、袋Cに4個入る」事象Eとでは起こりやすさが違うのです。
全事象は、10個の球をすべて異なると考え、10個の球の各1個について袋A,袋B,袋Cの3通りの入り方があるので、重複順列として、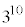 通りの入れ方があり、これらの各一通りは同様に確からしいと言えます。
通りの入れ方があり、これらの各一通りは同様に確からしいと言えます。
そのうち袋Aに3個、袋Bに2個はいるのは、まず10個から袋Aに入る3個を選ぶ方法が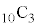 通り、残り7個から袋Bに入る2個を選ぶ方法が
通り、残り7個から袋Bに入る2個を選ぶ方法が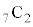 通り、これで袋Cに入る球が確定します。よって、袋Aに3個、袋Bに2個入る入れ方は、
通り、これで袋Cに入る球が確定します。よって、袋Aに3個、袋Bに2個入る入れ方は、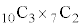 通り(同じものを含む順列を参照)。
通り(同じものを含む順列を参照)。
求める確率は、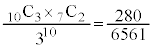 ......[答]
......[答]
注.10個の球が異なるとして、事象Dの場合の数は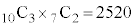 通り、事象Eの場合の数は
通り、事象Eの場合の数は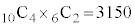 通りです。
通りです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 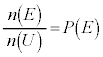 を、事象Eの起こる確率と言います。
を、事象Eの起こる確率と言います。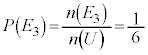 です。
です。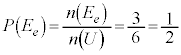 です。
です。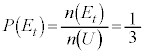 というように考えることもできます。ただし、ここで考えている3つの根元事象
というように考えることもできます。ただし、ここで考えている3つの根元事象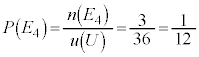 となります。
となります。