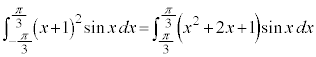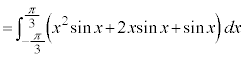偶関数・奇関数の積分 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
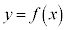 のグラフがy軸に関して対称であるとき、つまり、定義域内のxに関して、
のグラフがy軸に関して対称であるとき、つまり、定義域内のxに関して、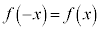 が成り立つとき、
が成り立つとき、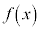 を偶関数と言う。
を偶関数と言う。
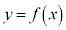 のグラフが原点に関して対称であるとき、つまり、定義域内のxに関して、
のグラフが原点に関して対称であるとき、つまり、定義域内のxに関して、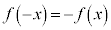 が成り立つとき、
が成り立つとき、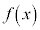 を奇関数と言う。
を奇関数と言う。
(1) 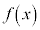 が偶関数であるとき、
が偶関数であるとき、
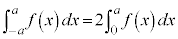
(2) 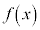 が奇関数であるとき、
が奇関数であるとき、
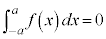
[証明](1)について、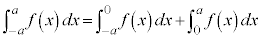
右辺第1項の積分は、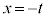 とおくと、
とおくと、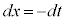 ,x:
,x: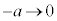 のとき、t:
のとき、t: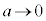 (置換積分を参照)
(置換積分を参照)
また、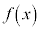 が偶関数であることから、
が偶関数であることから、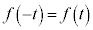 ,よって、
,よって、
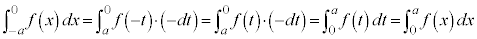
∴ 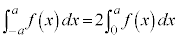
(2)について、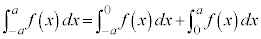
右辺第1項の積分は、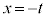 とおくと、
とおくと、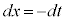 ,x:
,x: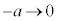 のとき、t:
のとき、t: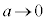
また、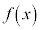 が奇関数であることから、
が奇関数であることから、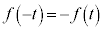 ,よって、
,よって、
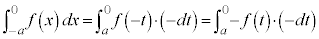
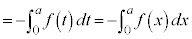
∴ 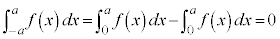
(証明終)
(1)は、偶関数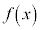 では、曲線
では、曲線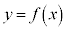 の
の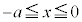 の部分と
の部分と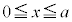 の部分とは同じ形をしています。
の部分とは同じ形をしています。
この2つの部分とx軸とに挟まれている部分の面積は等しいので、定積分の計算では、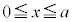 の部分を2倍すればよいのです。
の部分を2倍すればよいのです。
(2)は、奇関数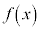 では、曲線
では、曲線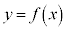 の
の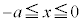 の部分と
の部分と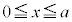 の部分とでは、同じ形ですが、符号がちょうど逆になっていて、
の部分とでは、同じ形ですが、符号がちょうど逆になっていて、
定積分についても、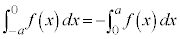 という関係にあるので、足し合わせれば0になるということです。
という関係にあるので、足し合わせれば0になるということです。
例.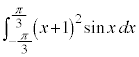 を計算する。
を計算する。
[解答] 積分区間が、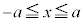 という風になっている場合には、必ず関数の偶奇に注意してください。
という風になっている場合には、必ず関数の偶奇に注意してください。
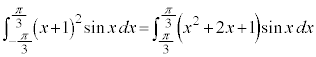
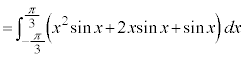
ここで、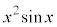 と
と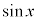 は奇関数なので、定積分は0になります。
は奇関数なので、定積分は0になります。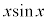 は偶関数なので、
は偶関数なので、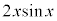 の定積分だけ、積分区間を
の定積分だけ、積分区間を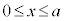 としたものを2倍にして計算すればよいのです。
としたものを2倍にして計算すればよいのです。
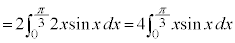
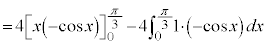
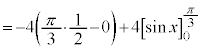
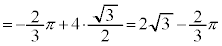 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 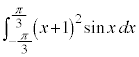 を計算する。
を計算する。