�����藝�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
��]�̒藝�F������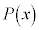 ��
��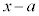 �Ŋ���ƁA�]���
�Ŋ���ƁA�]���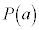
[�ؖ�]�@������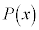 ��
��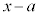 �Ŋ������Ƃ��̏���
�Ŋ������Ƃ��̏���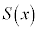 �C�]���R�Ƃ��܂��B
�C�]���R�Ƃ��܂��B
1�����Ŋ���̂ŁA�]��͒萔�ł�(�������̏��Z���Q��)�B
���̂Ƃ��A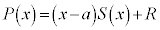
�����ŁA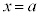 �Ƃ���ƁA
�Ƃ���ƁA
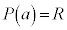
����āA������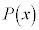 ��
��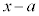 �Ŋ���ƁA�]���
�Ŋ���ƁA�]���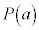 �@(�ؖ��I)
�@(�ؖ��I)
��1�D������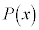 ��
��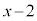 �Ŋ����3�]��A
�Ŋ����3�]��A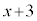 �Ŋ����
�Ŋ����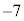 �]��Ƃ����B
�]��Ƃ����B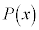 ��
��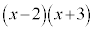 �Ŋ������]������߂�B
�Ŋ������]������߂�B
[��]�@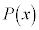 ��
��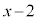 �Ŋ����3�]�邩��A
�Ŋ����3�]�邩��A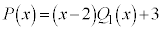 ����@ �Ƃ����܂��B
����@ �Ƃ����܂��B
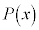 ��
��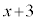 �Ŋ����
�Ŋ����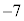 �]�邩��A��]�̒藝���A
�]�邩��A��]�̒藝���A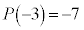 �ł��B
�ł��B
�@�ɂ����āA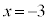 �Ƃ���ƁA
�Ƃ���ƁA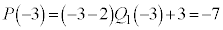
�� 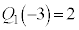
������A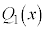 ��
��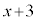 �Ŋ����2�]��̂ŁA
�Ŋ����2�]��̂ŁA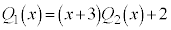 �Ƃ����܂��B
�Ƃ����܂��B
������@�ɑ������ƁA
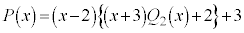
�@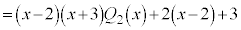
�@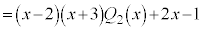
����āA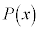 ��
��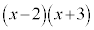 �Ŋ������]��́A
�Ŋ������]��́A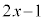 ......[��]
......[��]
[�ʉ�]�@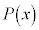 ��2����
��2����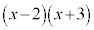 �Ŋ������]���1�����Ȃ̂ŁA
�Ŋ������]���1�����Ȃ̂ŁA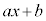 �Ƃ����ƁA
�Ƃ����ƁA
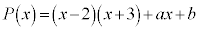 �@����A
�@����A
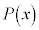 ��
��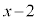 �Ŋ����3�]��̂ŁA�A��
�Ŋ����3�]��̂ŁA�A��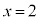 �Ƃ��āA��]�̒藝���A
�Ƃ��āA��]�̒藝���A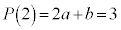 �@����B
�@����B
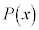 ��
��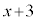 �Ŋ����
�Ŋ����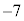 �]��̂ŁA�A��
�]��̂ŁA�A��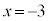 �Ƃ��āA��]�̒藝���A
�Ƃ��āA��]�̒藝���A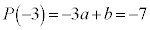 �@����C
�@����C
�B�|�C���A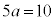 �@��
�@�� 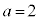
�B���A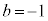
�����苁�߂�]��́A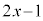 ......[��]
......[��]
������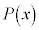 ��
��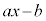 �Ŋ������Ƃ��̏���
�Ŋ������Ƃ��̏���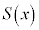 �C�]���R�Ƃ��āA
�C�]���R�Ƃ��āA
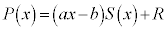
�����ŁA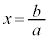 �Ƃ���ƁA
�Ƃ���ƁA
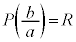
�����A������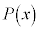 ��
��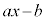 �Ŋ������Ƃ��̗]��́A
�Ŋ������Ƃ��̗]��́A �ł��B
�ł��B
�����藝�F������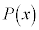 ��
��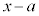 �Ŋ����� ��
�Ŋ����� �� 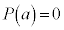
[�ؖ�]�@��]�̒藝���A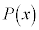 ��
��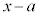 �Ŋ������Ƃ��̗]���
�Ŋ������Ƃ��̗]���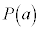
������Ƃ��A�]��
�t�ɁA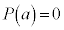 �̂Ƃ��A
�̂Ƃ��A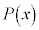 ��
��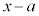 �Ŋ������Ƃ��̏���
�Ŋ������Ƃ��̏���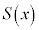 �Ƃ��āA
�Ƃ��āA
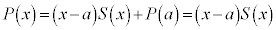
����āA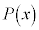 ��
��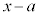 �Ŋ����܂��B�@(�ؖ��I)
�Ŋ����܂��B�@(�ؖ��I)
�����藝��p���āA��������������@���l���܂��B
�������F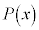 �ɂ��āA
�ɂ��āA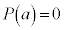 �ł���A
�ł���A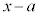 �Ŋ�����̂ŁA
�Ŋ�����̂ŁA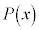 ��x�ɓK���Ȑ��la�������āA
��x�ɓK���Ȑ��la�������āA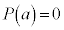 �ƂȂ���̂�T���܂��B
�ƂȂ���̂�T���܂��B
�����j�ɒT���Ă��Ȃ��Ȃ�������Ȃ��Ƃ�������̂ŁA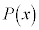 �̒萔����c�C�ō����̍��̌W����d�Ƃ��āAc�̖q�Ad�̖�Ƃ��镪����a�Ƃ��āA
�̒萔����c�C�ō����̍��̌W����d�Ƃ��āAc�̖q�Ad�̖�Ƃ��镪����a�Ƃ��āA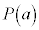 ���v�Z���A
���v�Z���A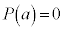 �ƂȂ�A
�ƂȂ�A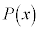 ��
��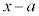 �Ŋ����܂��B
�Ŋ����܂��B
��2�D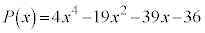 �������������Ă݂܂��B
�������������Ă݂܂��B
�萔����36�̖́A1�C2�C3�C4�C���
�ō����̍��̌W��4�̖́A1�C2�C4
�܂�1��ɂ�����̂���A1�C2�C3�C����C�Ə��ɑ�����Ă����܂��B
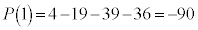 ���A
���A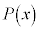 ��
��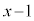 �Ŋ����܂���B
�Ŋ����܂���B
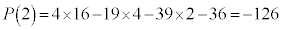 ���A
���A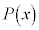 ��
��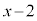 �Ŋ����܂���B
�Ŋ����܂���B
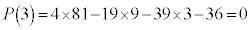 ���A
���A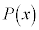 ��
��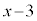 �Ŋ����܂��B
�Ŋ����܂��B
 ��
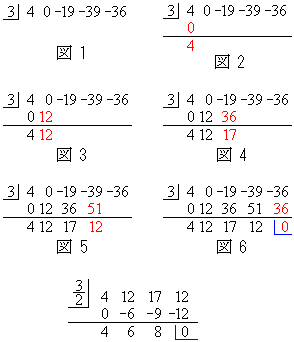
��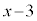 �Ŋ���܂����A1�����Ŋ���Ƃ��̊���Z�́A�E�}�̂悤�ɑg�ݗ��ď��@�ɂ��̂��֗��ł��B
�Ŋ���܂����A1�����Ŋ���Ƃ��̊���Z�́A�E�}�̂悤�ɑg�ݗ��ď��@�ɂ��̂��֗��ł��B
 ��
��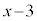 �Ŋ���̂ŁA�܂��A�����鎮�̌W�����o���ď����A3 (x���������)���ǂ����ɁA���ԈႢ�����Ȃ��悤�ɏ����܂�(�}1)�B
�Ŋ���̂ŁA�܂��A�����鎮�̌W�����o���ď����A3 (x���������)���ǂ����ɁA���ԈႢ�����Ȃ��悤�ɏ����܂�(�}1)�B
4�̉���0 (�ŏ���0�ł�)�������A4��0�̘a4�����̉��ɏ����܂�(�}2)�B
��̘a��4��3��������12��0�̉��ɏ����A0��12�̘a12�����̉��ɏ����܂�(�}3)�B
��̘a12��3��������36��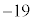 �̉��ɏ����A
�̉��ɏ����A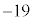 ��36�̘a17�����̉��ɏ����܂�(�}4)�B
��36�̘a17�����̉��ɏ����܂�(�}4)�B
��̘a17��3��������51��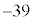 �̉��ɏ����A51��
�̉��ɏ����A51��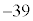 �̘a12�����̉��ɏ����܂�(�}5)�B
�̘a12�����̉��ɏ����܂�(�}5)�B
��̘a12��3��������36��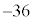 �̉��ɏ����A
�̉��ɏ����A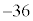 ��36�̘a0�����̉��ɏ����܂�(�}6)�B
��36�̘a0�����̉��ɏ����܂�(�}6)�B
�Ō��0�����͑������̏��Z�̗]��ł��B�]�肪�����0�ɂȂ�܂���B����0���������c��́A4�C12�C17�C12�͏��̊e���̌W���ł��B
�]���āA��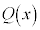 �́A
�́A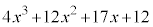 �ƂȂ�܂��B
�ƂȂ�܂��B
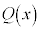 �̈����������l���܂��B
�̈����������l���܂��B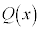 ��x�ɐ����������Ă�0�ɂȂ�Ȃ��͖̂��炩�ł��B
��x�ɐ����������Ă�0�ɂȂ�Ȃ��͖̂��炩�ł��B
x�ɕ����������Ă����܂��B
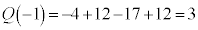 �C
�C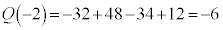 �C
�C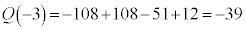 �C���
�C���
�����ŁA�����2�ɂ��Ă݂܂��B
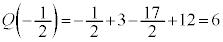 �C
�C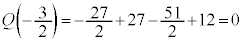
������A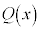 ��
��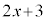 �Ŋ����܂��B���̂Ƃ��̑g�ݗ��ď��@�́A
�Ŋ����܂��B���̂Ƃ��̑g�ݗ��ď��@�́A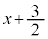 �Ŋ���ƍl���ĉE���}�̂悤�ɂ��܂��B
�Ŋ���ƍl���ĉE���}�̂悤�ɂ��܂��B
���́A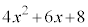 �ƂȂ�A
�ƂȂ�A

�@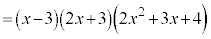
�ƈ�����������܂���(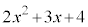 �͎����͈̔͂ł͈��������ł��܂���)�B
�͎����͈̔͂ł͈��������ł��܂���)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B