�d�ʑ吔�w'07�N���[3]
��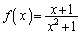 �ɂ��āA�ȉ��̖₢�ɓ�����B
�ɂ��āA�ȉ��̖₢�ɓ�����B
(1) 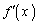 �C
�C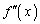 �����߂�B
�����߂�B (2) 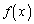 �̋ɒl�����߂�B
�̋ɒl�����߂�B (3) �Ȑ�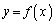 �Ƃ��̋Ȑ���̓_P
�Ƃ��̋Ȑ���̓_P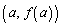 �ɂ�����ڐ��Ƃ��_P�̂ق��ɋ��L�_�������Ȃ��Ƃ���B���̂悤��a�̒l�����ׂċ��߂�B
�ɂ�����ڐ��Ƃ��_P�̂ق��ɋ��L�_�������Ȃ��Ƃ���B���̂悤��a�̒l�����ׂċ��߂�B (�ꕔ�ȗ�)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ƃ̖��̈ꕔ���폜���܂����B���Ƃ̖��ɂ́A�v�Z��(3)���������邽�߂̗U�������Ă���̂ł����A�����ł́A��ʓI�ɑΉ��ł���悤�ɁA�v�Z�ɂ��Ȃ��l���������݂܂��B
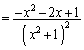 ......[��]
......[��]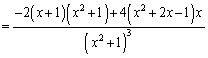
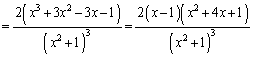 ......[��]
......[��]
(2) 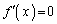 �Ƃ���ƁA
�Ƃ���ƁA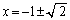
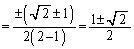 �@(��������)
�@(��������)�����\���A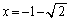 �ɂ����ċɏ��l�F
�ɂ����ċɏ��l�F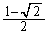 �C
�C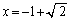 �ɂ����ċɑ�l�F
�ɂ����ċɑ�l�F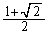 ......[��]�@(���̑������Q��)
......[��]�@(���̑������Q��)
(3) 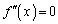 �Ƃ���ƁA
�Ƃ���ƁA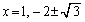
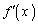 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B�����ŁA
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B�����ŁA �ł��B
�ł��B
�Ȍ�A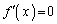 �̉���
�̉���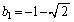 �C
�C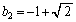 (
(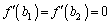 )�C
)�C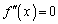 �̉���
�̉���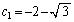 �C
�C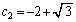 �C
�C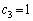 (
(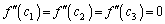 )�Ƃ����܂��B
)�Ƃ����܂��B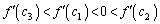 �ł��B
�ł��B
�܂��A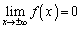 �C
�C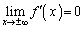 �ł��B�@����@
�ł��B�@����@
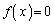 �̉���
�̉���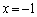 �C
�C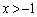 �ɂ�����
�ɂ�����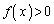 �C
�C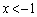 �ɂ�����
�ɂ�����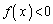 �@����A
�@����A
���āA��ӂ��A�ƁA�_P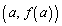 �ɂ�����ڐ�
�ɂ�����ڐ� ��A�����A
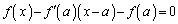 �@(���ӂ�
�@(���ӂ�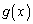 �Ƃ����܂�)�@����B
�Ƃ����܂�)�@����B�Ƃ���ƁA���̕�����(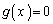 )�́A
)�́A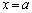 (���ꂪ���ł��邱�Ƃ͖��炩�ł�)�ȊO�̉��������܂���B
(���ꂪ���ł��邱�Ƃ͖��炩�ł�)�ȊO�̉��������܂���B
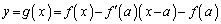 �̃O���t�ׂĂ݂܂��B
�̃O���t�ׂĂ݂܂��B ����āA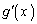 ��
��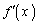 �Ɠ��l�Ɉȉ��̑����\�̂悤�ɕω����܂��B�����ŁA
�Ɠ��l�Ɉȉ��̑����\�̂悤�ɕω����܂��B�����ŁA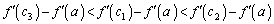 �Ȃ̂ŁA
�Ȃ̂ŁA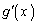 �́A
�́A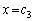 �ɂ����čŏ��l
�ɂ����čŏ��l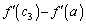 ���Ƃ�A
���Ƃ�A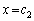 �ɂ����čő�l
�ɂ����čő�l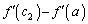 ���Ƃ�܂��B
���Ƃ�܂��B
������A (i) 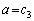 �̂Ƃ��A�ŏ��l
�̂Ƃ��A�ŏ��l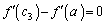 ���A
���A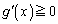 �ł���A
�ł���A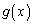 �͑������ł��B�]���āA
�͑������ł��B�]���āA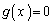 �C�����B�́A
�C�����B�́A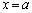 �ȊO�̉��������܂���B
�ȊO�̉��������܂���B (ii) 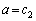 �̂Ƃ��A�ő�l
�̂Ƃ��A�ő�l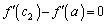 ���A
���A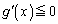 �ł���A
�ł���A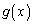 �͌������ł��B�]���āA
�͌������ł��B�]���āA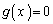 �C�����B�́A
�C�����B�́A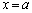 �ȊO�̉��������܂���B
�ȊO�̉��������܂���B (iii) 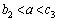 �̂Ƃ��A
�̂Ƃ��A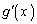 �̑����\���A
�̑����\���A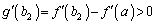 �C
�C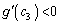 �C
�C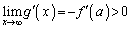 ���A������
���A������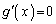 �́A
�́A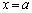 �ȊO�ɁA
�ȊO�ɁA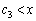 �͈̔͂ɂ���1��d�������܂��B
�͈̔͂ɂ���1��d�������܂��B ������A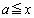 �ɂ�����
�ɂ�����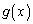 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A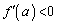 �C�܂��@���A
�C�܂��@���A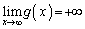 �ł��B
�ł��B
�����\���A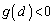 �ł���A������
�ł���A������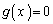 �́A
�́A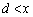 �͈̔͂�
�͈̔͂�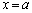 �ȊO�̉������̂ŁA�s�K�ł��B
�ȊO�̉������̂ŁA�s�K�ł��B (iv) 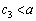 �̂Ƃ��A
�̂Ƃ��A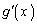 �̑����\���A
�̑����\���A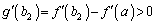 �C
�C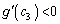 �C
�C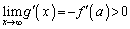 ���A������
���A������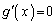 �́A
�́A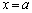 �ȊO�ɁA
�ȊO�ɁA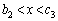 �͈̔͂ɂ���1��d�������܂��B
�͈̔͂ɂ���1��d�������܂��B ������A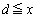 �ɂ�����
�ɂ�����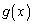 �̑����\(
�̑����\(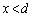 �ɂ����Ă�
�ɂ����Ă�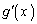 �͐��ɂȂ����蕉�ɂȂ����肷��\��������܂�)�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A
�͐��ɂȂ����蕉�ɂȂ����肷��\��������܂�)�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A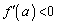 �C�܂��@���A
�C�܂��@���A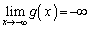 �ł��B
�ł��B
�����\���A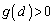 �ł���A������
�ł���A������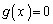 �́A
�́A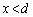 �͈̔͂�
�͈̔͂�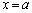 �ȊO�̉������̂ŁA�s�K�ł��B
�ȊO�̉������̂ŁA�s�K�ł��B (v) 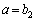 �̂Ƃ��A
�̂Ƃ��A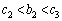 �ł����A
�ł����A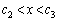 �ɂ�����
�ɂ�����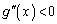 ���
���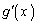 �͌������ŁA
�͌������ŁA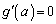 �ł������̑O���
�ł������̑O���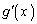 �̕����͐����畉�ɕς��A
�̕����͐����畉�ɕς��A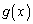 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B 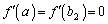 �C
�C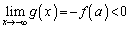 (�� �A)�Ƒ����\���A������
(�� �A)�Ƒ����\���A������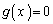 �C�����B�́A
�C�����B�́A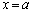 �ȊO�̉��������܂���B
�ȊO�̉��������܂���B(vi) 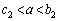 �̂Ƃ��A
�̂Ƃ��A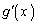 �̑����\���A
�̑����\���A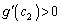 �C
�C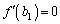 ��
��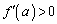 ���
���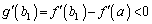 �C�]���āA������
�C�]���āA������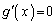 �́A
�́A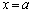 �ȊO�ɁA
�ȊO�ɁA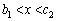 �͈̔͂ɂ���1��d�������܂��B
�͈̔͂ɂ���1��d�������܂��B ������A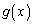 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A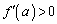 �C�܂��@���A
�C�܂��@���A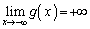 �ł��B
�ł��B
�����\���A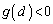 �ł���A������
�ł���A������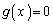 �́A
�́A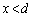 �͈̔͂�
�͈̔͂�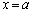 �ȊO�̉������̂ŁA�s�K�ł��B
�ȊO�̉������̂ŁA�s�K�ł��B (vii) 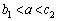 �̂Ƃ��A
�̂Ƃ��A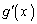 �̑����\���A
�̑����\���A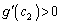 �C
�C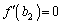 ��
��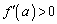 ���
���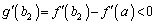 �C�]���āA������
�C�]���āA������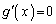 �́A
�́A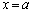 �ȊO�ɁA
�ȊO�ɁA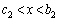 �͈̔͂ɂ���1��d�������܂��B
�͈̔͂ɂ���1��d�������܂��B ������A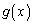 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A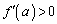 �C�܂��@���A
�C�܂��@���A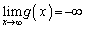 �ł��B
�ł��B
�����\���A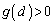 �ł���A������
�ł���A������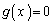 �́A
�́A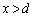 �͈̔͂�
�͈̔͂�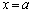 �ȊO�̉������̂ŁA�s�K�ł��B
�ȊO�̉������̂ŁA�s�K�ł��B (viii) 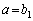 �̂Ƃ��A
�̂Ƃ��A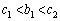 �ł����A
�ł����A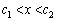 �ɂ�����
�ɂ�����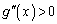 ���
���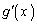 �͑������ŁA
�͑������ŁA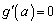 �ł������̑O���
�ł������̑O���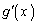 �̕����͕����琳�ɕς��A
�̕����͕����琳�ɕς��A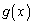 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B 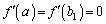 �C
�C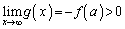 (�� �A)�Ƒ����\���A������
(�� �A)�Ƒ����\���A������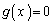 �C�����B�́A
�C�����B�́A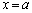 �ȊO�̉��������܂���B
�ȊO�̉��������܂���B(ix) 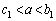 �̂Ƃ��A
�̂Ƃ��A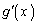 �̑����\���A
�̑����\���A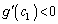 �C
�C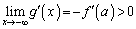 ���A������
���A������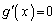 �́A
�́A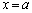 �ȊO�ɁA
�ȊO�ɁA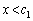 �͈̔͂ɂ���1��d�������܂��B
�͈̔͂ɂ���1��d�������܂��B ������A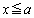 �ɂ�����
�ɂ�����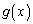 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A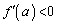 �C�܂��@���A
�C�܂��@���A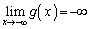 �ł��B
�ł��B
�����\���A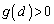 �ł���A������
�ł���A������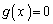 �́A
�́A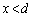 �͈̔͂�
�͈̔͂�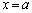 �ȊO�̉������̂ŁA�s�K�ł��B
�ȊO�̉������̂ŁA�s�K�ł��B �܂��A�A��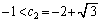 ���A
���A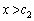 �ɂ����āA
�ɂ����āA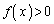 �C
�C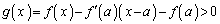
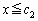 �ɂ����鑝���\�́A�ȉ��̂悤�ɂȂ�܂��B�ȏ���A������
�ɂ����鑝���\�́A�ȉ��̂悤�ɂȂ�܂��B�ȏ���A������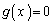 �C�����B�́A
�C�����B�́A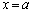 �ȊO�̉��������܂���B
�ȊO�̉��������܂���B (xi) 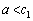 �̂Ƃ��A
�̂Ƃ��A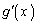 �̑����\���A
�̑����\���A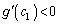 �C
�C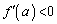 ���
���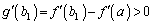 �ƂȂ�̂ŁA������
�ƂȂ�̂ŁA������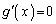 �́A
�́A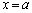 �ȊO�ɁA
�ȊO�ɁA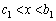 �͈̔͂ɂ���1��d�������܂��B
�͈̔͂ɂ���1��d�������܂��B ������A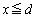 �ɂ�����
�ɂ�����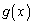 �̑����\(
�̑����\(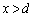 �ɂ����Ă�
�ɂ����Ă�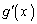 �͐��ɂȂ����蕉�ɂȂ����肵�܂�)�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A
�͐��ɂȂ����蕉�ɂȂ����肵�܂�)�͈ȉ��̂悤�ɂȂ�܂��B���̂Ƃ��A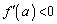 �C�܂��@���A
�C�܂��@���A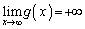 �ł��B
�ł��B
�����\���A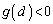 �ł���A������
�ł���A������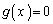 �́A
�́A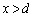 �͈̔͂�
�͈̔͂�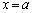 �ȊO�̉������̂ŁA�s�K�ł��B
�ȊO�̉������̂ŁA�s�K�ł��B �ȏ�ł��ׂĂ̏ꍇ�ׂ܂������A���߂�a�̒l�́A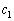 �C
�C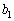 �C
�C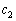 �C
�C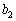 �C
�C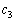 �C�܂�A
�C�܂�A
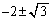 �C
�C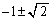 �C1 ......[��]
�C1 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 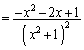 ......[��]
......[��]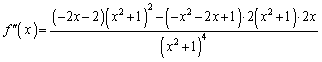
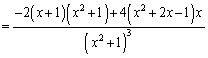
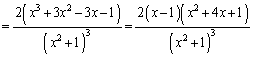 ......[��]
......[��]