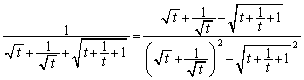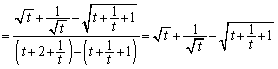名市大経済数学'08年[4]
正の数xに対して、三辺の長さが
で与えられる三角形ABCを考える。次の問いに答えよ。
(1) 
のとき、三角形ABCが存在するようなkの値の範囲を求めよ。 (2) 任意の正の数tに対して不等式
･･･①および
･･･②が成立することを示せ。ただし、②を証明する際に①を利用してよい。
(3) (2)の結果を利用して、任意の正の数xに対して三角形ABCが存在するようなkの値の範囲を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 センター試験を意識して、相加平均・相乗平均の関係の利用法を考えてみましょう。(2)は、「②を証明する際に①を利用してよい」というヒントがないと、まごつくかも知れません。
(1) 
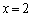のとき、 
なので、三角形ABCが存在する条件(2辺の和>他の1辺)は、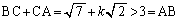
･･･③かつ
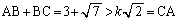･･･④です。③より、
④より、
以上より、
......[答]
(2) 相加平均・相乗平均の関係より、
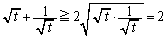･･･⑤不等号の等号は、
，つまり、
のときに成立します。
相加平均・相乗平均の関係より、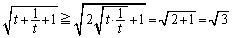 
･･･⑥不等号の等号は、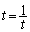
，つまり、
のときに成立します。
⑤，⑥を辺々加えることにより、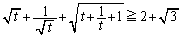 
(不等号の等号は
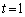のときに成立)不等式①が成立します。また、これより、
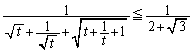･･･⑦右辺は、
ですが、左辺は、
よって、⑦より、
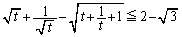(不等号の等号は
のときに成立)不等式②が成立します。
注．⑤－⑥としても、不等式②を示すことはできません。
は成り立たないからです。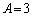
，
，
，
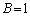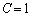のときを考えてください。
もちろん、 も言えません。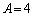
，
，
，
のときを考えてください。
また、上記では、⑤＋⑥を作ることによって、不等式①を導いたのですが、これができたのは、⑤と⑥の等号成立条件が同じだからです。同じでなければ、⑤＋⑥から①を導くことはできません。例えば、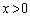
のとき、相加平均・相乗平均の関係より、 
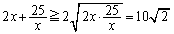･･･(a)ですが、だからと言って、
･･･(b)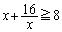
･･･(c)の2式を辺々加え合わせて、
(
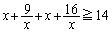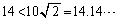)としても、(a)は導けないのです。
なぜかと言うと、(b)の等号成立条件は、
，つまり、
(c)の等号成立条件は、
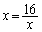，つまり、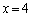
で等号成立条件が異なるからです。
(3) 
より、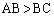
なので、三角形ABCが存在する条件は、
･･･⑧かつ
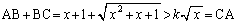･･･⑨です。⑧より、
この不等式の右辺は(2)より
以下なので、 であれば、⑧は、任意の正の数xについて成り立ちます。
⑨より、
この不等式の右辺は(2)より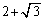
以上なので、 であれば、⑨は、任意の正の数xについて成り立ちます。
以上より、任意の正の数xに対して三角形ABCが存在するようなkの値の範囲は、
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
，
，
かつ
” ⇒ “
”
かつ
” ⇒ “
”
