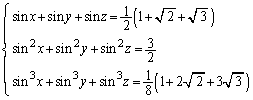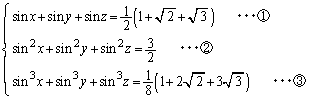�����㐔�w'09�N[1]
���̖₢�ɓ�����B
(1) x��3�������� (
( )��3�̉���α�Cβ�Cγ�Ƃ���Ƃ��A���ƌW���̊W�������A������ؖ�����B
)��3�̉���α�Cβ�Cγ�Ƃ���Ƃ��A���ƌW���̊W�������A������ؖ�����B (2) 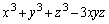 �������͈̔͂ň�����������B
�������͈̔͂ň�����������B (3) x�Cy�Cz�Ɋւ��鎟�̘A���������������B
�������A �Ƃ���B
�Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ƌW���̊W�����܂����p����3���������������A�Ƃ������ł��B
x��3�������� ��3�̉���α�Cβ�Cγ�̂Ƃ��A
��3�̉���α�Cβ�Cγ�̂Ƃ��A �ƈ��������ł��܂��B�E�ӂ�W�J����ƁA
���ӊe���̌W�����r���āA
������A���ƌW���̊W���������܂��B�@(�ؖ��I)
��W�J���Ă݂܂��B
�� 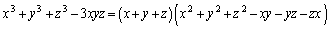 ......[��]
......[��]
(3) 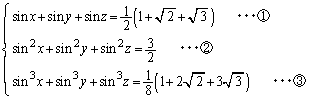
�@��2�悵�āA
�A��p���āA
 �@����C
�@����C(2)�̌��ʂ�p���āA
�B�C�@�C�A�C�C�������āA
��  �@����D
�@����D
�@�C�C�C�D���A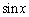 �C
�C �C
�C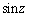 ��3���Ƃ���3���������́A(1)�̌��ʂ�p���āA
��3���Ƃ���3���������́A(1)�̌��ʂ�p���āA  �@����E
�@����E �Ə�����̂ŁA3����
�Ə�����̂ŁA3���� �C
�C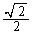 �C
�C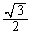 �炵���A�Ƃ������ƂɂȂ�܂����A���ۂɁA�E���ӂ�t �̌W���ɂ��āA
�炵���A�Ƃ������ƂɂȂ�܂����A���ۂɁA�E���ӂ�t �̌W���ɂ��āA�ƂȂ�̂ŁA�E���ӂ�������������ƁA
 ���A
���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B