3次方程式の解と係数の関係 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
3次方程式：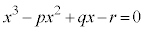
の3解がα，β，γだとすると、
，
，
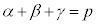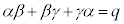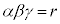
[証明]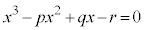 
･･･① の3解がα，β，γのとき、
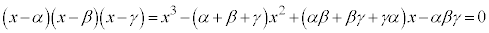･･･②
①，②各項の係数を比較して、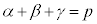
，
，
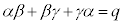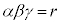(証明終)
3次関数の解と係数の関係に出てくる、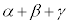
，
，
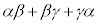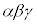は、3文字の場合の基本対称式になっています。
3次関数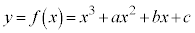
･･･③ を考えます。
導関数は、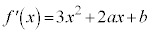
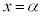における接線の方程式は、
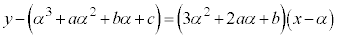･･･④
このとき、接線④と、もとの曲線③との交点を求める問題があります。
この問題で、素直に、③と④を連立して解いても、重解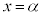
をもつことがわかっているので、もう一つの解を求めることはそれほど大変ではありません。
ですが、交点のx座標をβとすれば、③と④を連立してできる3次方程式の3解は、α，α，βなので、解と係数の関係を使って、
∴ 
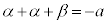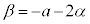
と即座に求まるので便利です。
そのほか、3次方程式の3解の間に条件が指定されている問題があります。こうした問題では、解と係数の関係を使います。
[例] 3次方程式：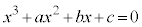
の3実数解をα，β，γとして、βが他の2解の相加平均になっている場合、
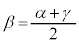と解と係数の関係から、
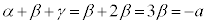より、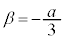
となります。
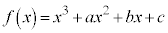として、
，
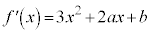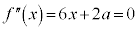とすると、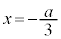
となりますが、
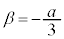は、変曲点のx座標になっています。これは、3次関数のグラフが変曲点に関して対称であることを考えれば納得がいくでしょう。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。