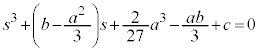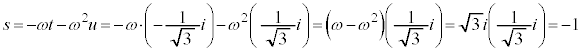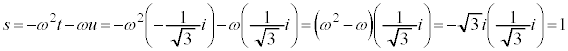3次方程式 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
3次方程式: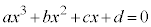 (a,b,c,dは実数,
(a,b,c,dは実数,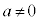 ) ・・・①
) ・・・①
の解は、左辺が因数分解できるなら、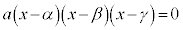 より、
より、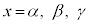 の3解です。
の3解です。
このとき、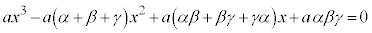
より、係数比較して、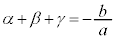 ,
,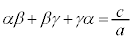 ,
,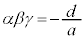 が成立します(解と係数の関係と言います)。
が成立します(解と係数の関係と言います)。
因数分解の過程で、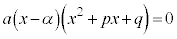 となるとき、
となるとき、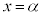 または
または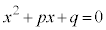 ,ですが、
,ですが、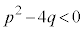 の場合、
の場合、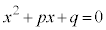 は実数解を持ちません。このときは、3次方程式の実数解は
は実数解を持ちません。このときは、3次方程式の実数解は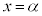 のみです。複素数の範囲では、
のみです。複素数の範囲では、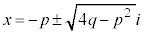 (iは虚数単位)の2個の複素数解があります。
(iは虚数単位)の2個の複素数解があります。
因数分解がすぐにできない場合には、因数定理を利用します。aの約数m,dの約数nから有理数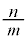 を作り、①の左辺のxに代入して0になるかどうか確かめます。0になれば、
を作り、①の左辺のxに代入して0になるかどうか確かめます。0になれば、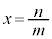 という解があり、
という解があり、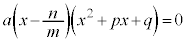 と因数分解されます。
と因数分解されます。
3次関数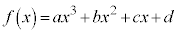 を考えます。ここでは、
を考えます。ここでは、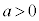 とします。
とします。
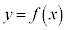 のグラフは全実数xに対して連続で、
のグラフは全実数xに対して連続で、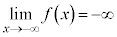 ,
,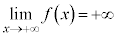 ・・・② より、少なくとも1つ
・・・② より、少なくとも1つ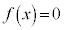 となるxがあり、3次方程式
となるxがあり、3次方程式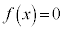 は少なくとも1つの実数解を持ちます。
は少なくとも1つの実数解を持ちます。
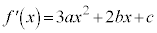
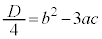 として、
として、
・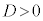 のとき、
のとき、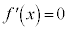 は、2個の実数解s,t (
は、2個の実数解s,t (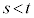 )を持ちます。増減表は以下のようになります。
)を持ちます。増減表は以下のようになります。 (a) 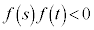 のとき、つまり、
のとき、つまり、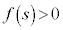 かつ
かつ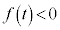 のとき、②と合わせて、3次方程式
のとき、②と合わせて、3次方程式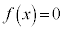 は、
は、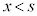 に1実数解、
に1実数解、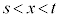 に1実数解、
に1実数解、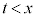 に1実数解、合わせて3実数解を持ちます。
に1実数解、合わせて3実数解を持ちます。 (b) 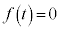 のとき、3次方程式
のとき、3次方程式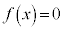 は、
は、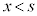 に1実数解、重解
に1実数解、重解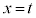 を持ちます。
を持ちます。 (c) 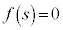 のとき、3次方程式
のとき、3次方程式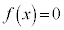 は、重解
は、重解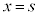 ,
,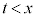 に1実数解を持ちます。
に1実数解を持ちます。 (d) 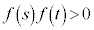 のとき、
のとき、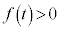 なら、3次方程式
なら、3次方程式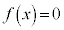 は、
は、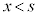 に1実数解を持ちます。
に1実数解を持ちます。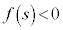 なら、3次方程式
なら、3次方程式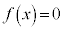 は、
は、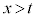 に1実数解を持ちます。
に1実数解を持ちます。 ・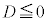 のとき、
のとき、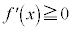 または
または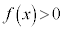 ですが、
ですが、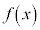 は単調増加関数で、3次方程式
は単調増加関数で、3次方程式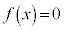 は、ただ1つの実数解を持ちます。
は、ただ1つの実数解を持ちます。
3次方程式の一般解法は、16世紀の数学者カルダノの方法が知られています('94日本医科大に出題)。
まず、3次方程式の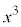 の係数で方程式を割って、
の係数で方程式を割って、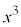 の係数を1にします。
の係数を1にします。
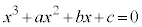
になったとします。ここで、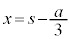 と置いて、
と置いて、
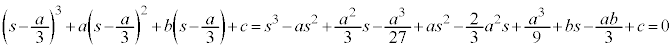
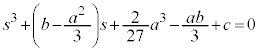
として、2乗の項を消します。さらに、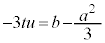 ,
,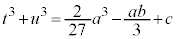 とおくと、
とおくと、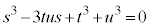
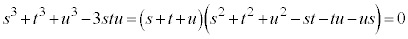
2個目のカッコ内を因数分解するために、1の3乗根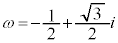 を導入します。
を導入します。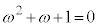 より、
より、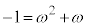 となるので、
となるので、
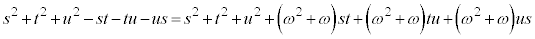
こうして、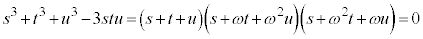
∴ 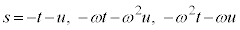 ・・・③
・・・③
[例1] 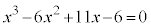 では、
では、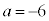 ,
,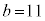 ,
,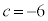 として、
として、
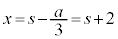 とおくと、
とおくと、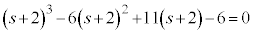
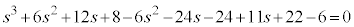
整理して、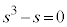
sの係数を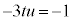 (
(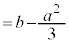 ),定数項を
),定数項を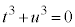 (
(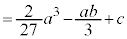 )とおくと、
)とおくと、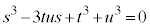
となり、③が3解を与えます。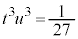 より、
より、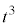 ,
,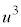 は、
は、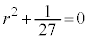 の2解で、
の2解で、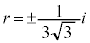
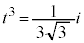 ,
,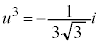 とすると、
とすると、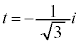 ,
,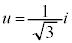
③に代入すると、
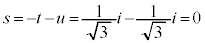
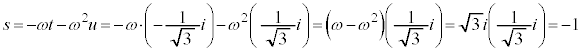
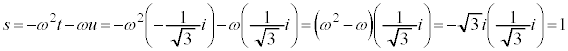
こうして、3次方程式の解は、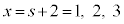
[例2] 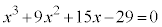 (上記の'94日本医科大で出題された方程式)では、
(上記の'94日本医科大で出題された方程式)では、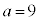 ,
,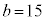 ,
,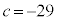 として、
として、
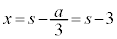 とおくと、
とおくと、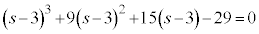
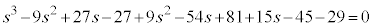
整理して、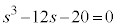
sの係数を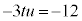 (
(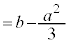 ),定数項を
),定数項を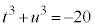 (
(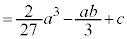 )とおくと、
)とおくと、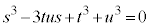
となり、③が3解を与えます。 より、
より、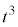 ,
,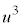 は、
は、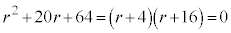 の2解で、
の2解で、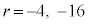
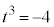 ,
,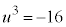 とすると、
とすると、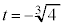 ,
,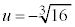
③に代入すると、
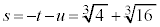
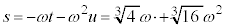
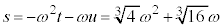
こうして、3次方程式の解は、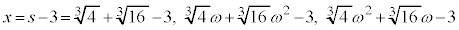
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。