�ޗnj�����吔�w'09�N[1]
xyz��Ԃɂ����Č��_O �𒆐S�Ƃ��锼�a1�̋��ʂ�S�Ƃ��A����S����_N
�𒆐S�Ƃ��锼�a1�̋��ʂ�S�Ƃ��A����S����_N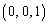 �������������ɑ�����_P
�������������ɑ�����_P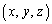 �ɑ��āA2�_N�CP��ʂ钼����xy����
�ɑ��āA2�_N�CP��ʂ钼����xy����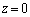 �Ƃ̌�_��Q�Ƃ����B
�Ƃ̌�_��Q�Ƃ����B
(1) �_Q�̍��W�����߂�B
(2) ����S��̔C�ӂ̓_R�ɑ���R�̂ǂ�ȋ߂��ɂ��AS��̓_ �Ŋe���Wa�Cb�Cc�����ׂėL��������Ȃ���̂����݂��邱�Ƃ��ؖ�����B
�Ŋe���Wa�Cb�Cc�����ׂėL��������Ȃ���̂����݂��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�����ł����A�u���������_�����݂��邱�Ɓv���ؖ��́A���������_�����߂���@�E�菇���������悢�̂ł��B�w�肳�ꂽ�菇�ɂ����������_���߂邱�Ƃ��ł���A�Ƃ������Ƃ́A���������_�����݂���A�Ƃ������Ƃł��B
(1) 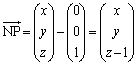
����NP��xy���ʂƂ̌�_�ɂ����ẮA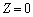 �Ƃ��āA
�Ƃ��āA �_P�͓_N�ƈقȂ�_�Ȃ̂ŁA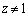
�� 
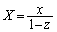 �C
�C
����āA�_Q�̍��W�́A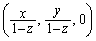 ......[��]
......[��]
(2) ����S��̔C�ӂ̓_R�ɂ��āA�_R���_N �̈ʒu�ɗ���悤�ɉ�]�����čl���邱�Ƃɂ���A�_R���_N���Ƃ��čl���Ĉ�ʐ��������܂���B
�̈ʒu�ɗ���悤�ɉ�]�����čl���邱�Ƃɂ���A�_R���_N���Ƃ��čl���Ĉ�ʐ��������܂���B �����ŁA�_N�̂ǂ�ȋ߂��ɂ��AS��̓_A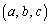 �Ŋe���Wa�Cb�Cc�����ׂėL��������Ȃ���̂����݂��邱�Ƃ��ؖ����邱�Ƃɂ��܂��B
�Ŋe���Wa�Cb�Cc�����ׂėL��������Ȃ���̂����݂��邱�Ƃ��ؖ����邱�Ƃɂ��܂��B
�܂��A�u�_N�̂ǂ�ȋ߂��ɂ��v�Ƃ����\�����A�_N�̂ǂ�ȋ߂��ɓ_N�Ƃ͈قȂ�_P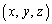 ���Ƃ����Ƃ��ɂ��A
���Ƃ����Ƃ��ɂ��A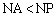 �����_A
�����_A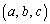 (a�Cb�Cc�͗L����)�����݂���A�Ƃ��čl���܂��B
(a�Cb�Cc�͗L����)�����݂���A�Ƃ��čl���܂��B
�����ŁA�_P�� �̕����ɂƂ�ꍇ�ɂ́A�_
�̕����ɂƂ�ꍇ�ɂ́A�_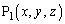 �̑���ɓ_
�̑���ɓ_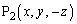 ��_P�Ƃ��čl����A
��_P�Ƃ��čl����A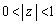 ���A
���A �Ȃ̂ŁA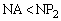 �ł����
�ł����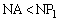 �ł��B
�ł��B
�����ŁA�_P�� �͈̔͂ɂƂ��čl���邱�Ƃɂ��܂��B
�͈̔͂ɂƂ��čl���邱�Ƃɂ��܂��B
����S��� �̕����ɂ�����N�Ƃ͈قȂ�C�ӂ̓_P�ɑ��A(1)���A����NP��xy���ʂƂ̌�_Q��
�̕����ɂ�����N�Ƃ͈قȂ�C�ӂ̓_P�ɑ��A(1)���A����NP��xy���ʂƂ̌�_Q��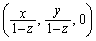 �ł��B�����ŁA
�ł��B�����ŁA 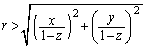 �@����@
�@����@�����L����r (�ǂ�Ȏ����ɑ��Ă��A��������傫�ȗL�����͕K�����݂��܂�)�ƗL����k (k�͉��ł��悢)���Ƃ��āA
 �C
�C
�Ƃ���AX�CY�͗L�����ł����āA
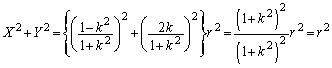 �@����A
�@����A���̂Ƃ��A����S��̓_A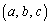 �ŁA����NA��xy���ʂƂ̌�_��
�ŁA����NA��xy���ʂƂ̌�_��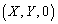 �ƂȂ�_���l���܂�(�_A��N�Ƃ͈قȂ�A�܂��A
�ƂȂ�_���l���܂�(�_A��N�Ƃ͈قȂ�A�܂��A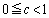 �Ƃ��܂�)�B(1)�Ɠ��l�ɁA
�Ƃ��܂�)�B(1)�Ɠ��l�ɁA  �C
�C
�܂�A
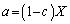 �C
�C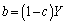 �@����B
�@����B�_A�͋���S��̓_�Ȃ̂ŁA
�A��p���āA
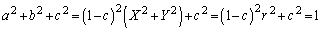 �@����C
�@����C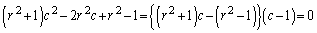
 ���A
���A �@����D
�@����D
�ƂȂ�Ar�͗L�����Ȃ̂ŁAc�͗L�����ł��B����āA�B���Aa�Cb���L�����ł��B �@(�� �D)�@����E
�@(�� �D)�@����E�@�̉E�ӂ�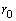 �Ƃ����ƁA
�Ƃ����ƁA �_P�͋���S��̓_�Ȃ̂ŁA
�C�Ɠ��l�ɂ��āA
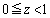 ���A
���A
�E�Ɠ��l�ɂ��āA�@�F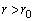 ���
��� ����́A�C�ӂ̓_P�ɑ���P����N�ɋ߂��_A�����݂��邱�Ƃ��Ӗ����܂��B
�����A�_N�̂ǂ�ȋ߂��ɂ��AS��̓_A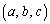 �Ŋe���Wa�Cb�Cc�����ׂėL����
�Ŋe���Wa�Cb�Cc�����ׂėL���� ����Ȃ���̂����݂��A��ӂ͏ؖ�����܂����B(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 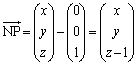
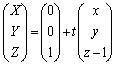
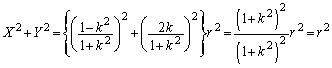 �@����A
�@����A