�É��嗝�n���w'09�N[1]
���̖₢�ɓ�����B
(1) ���ׂĂ̎��R��n�ɑ��āA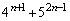 ��21�Ŋ����邱�Ƃ��ؖ�����B
��21�Ŋ����邱�Ƃ��ؖ�����B (2) ���̏��������萔�łȂ�������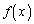 �𐄒肵�A���̐��肪���������Ƃ��ؖ�����B
�𐄒肵�A���̐��肪���������Ƃ��ؖ�����B (a) 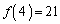
(b) ���ׂĂ̎��R��n�ɑ��āA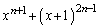 ��
��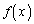 �Ŋ�����B
�Ŋ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(2)�͕��}�ɂ���Ă��ł��܂����A�����藝�𗘗p����ƃ��N�ɏؖ����ł��܂��B
(�T) 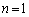 �̂Ƃ��A
�̂Ƃ��A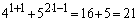 ��21�Ŋ�����̂ŁA���藧���܂��B
��21�Ŋ�����̂ŁA���藧���܂��B (�U) 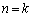 �̂Ƃ����藧�Ɖ��肷��ƁA
�̂Ƃ����藧�Ɖ��肷��ƁA 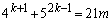 (m�F����)�@����@
(m�F����)�@����@�Ƃ������Ƃ��ł��܂��B
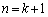 �̂Ƃ��A
�̂Ƃ��A �́A21�Ŋ�����̂ŁA���藧���܂��B
(�T)�C(�U)���A���ׂĂ̎��R��n�ɑ��āA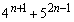 ��21�Ŋ����܂��B(�ؖ��I)
��21�Ŋ����܂��B(�ؖ��I)
(2) 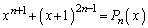 �Ƃ����܂��B
�Ƃ����܂��B 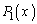 �C
�C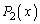 ���Ƃ��Ɋ���鑽������
���Ƃ��Ɋ���鑽������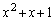 �Ȃ̂ŁA
�Ȃ̂ŁA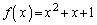 �Ɛ��肷�邱�Ƃ��ł��܂��B
�Ɛ��肷�邱�Ƃ��ł��܂��B���A����(a)�͖�������Ă��܂��B
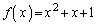 ������(b)�������Ƃ��A���w�I�A�[�@�ŏؖ����܂��B
������(b)�������Ƃ��A���w�I�A�[�@�ŏؖ����܂��B (�T) 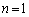 �̂Ƃ��A
�̂Ƃ��A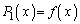 �́A
�́A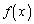 �Ŋ����܂��B
�Ŋ����܂��B (�U) 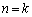 �̂Ƃ��A
�̂Ƃ��A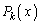 ��
��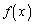 �Ŋ�����Ɖ��肷��ƁA
�Ŋ�����Ɖ��肷��ƁA 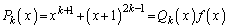 �@����A
�@����A�Ƃ������Ƃ��ł��܂��B�A���A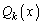 ��x�̑������ł��B
��x�̑������ł��B ����āA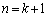 �̂Ƃ����A
�̂Ƃ����A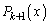 ��
��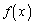 �Ŋ����܂��B
�Ŋ����܂��B (�T)�C(�U)���A���ׂĂ̎��R��n�ɑ��āA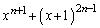 �́A
�́A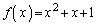 �Ŋ����܂��B(�ؖ��I)�ʉ��D
�Ŋ����܂��B(�ؖ��I)�ʉ��D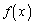 ������(b)�������Ƃɂ��ẮA�ȉ��̂悤�ɏؖ����邱�Ƃ��ł��܂��B
������(b)�������Ƃɂ��ẮA�ȉ��̂悤�ɏؖ����邱�Ƃ��ł��܂��B
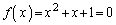 �̉��́A
�̉��́A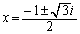
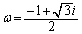 �Ƃ���ƁA
�Ƃ���ƁA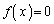 ��2���́A
��2���́A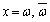 �ł��B�܂�A
�ł��B�܂�A 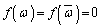 �@����B
�@����B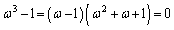 ���A
���A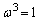 �C�܂��A
�C�܂��A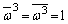
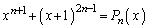 �Ƃ����ƁA�B���A
�Ƃ����ƁA�B���A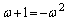 �䂦�A
�䂦�A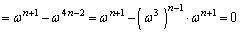 �@(��
�@(�� 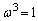 )
)����āA�����藝���A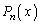 �́A
�́A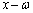 �ł�
�ł�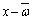 �ł������āA
�ł������āA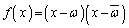 �Ŋ����܂��B
�Ŋ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B