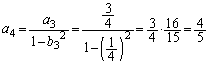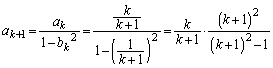���Q�嗝�n���w'10�N[3]
2�̐���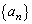 �C
�C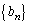 �́A���ׂĂ̎��R��n�ɂ���
�́A���ׂĂ̎��R��n�ɂ���
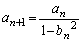 �C�@
�C�@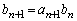
(1) ������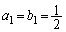 �ł���Ƃ���B
�ł���Ƃ���B (ii) 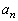 �C
�C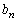 ��\��n�̎��𐄒肵�A�����̐��肪���������Ƃ𐔊w�I�A�[�@�ɂ���ďؖ�����B
��\��n�̎��𐄒肵�A�����̐��肪���������Ƃ𐔊w�I�A�[�@�ɂ���ďؖ�����B (2) ������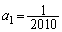 �C
�C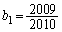 �ł���Ƃ���B
�ł���Ƃ���B (ii) 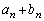 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��^�I�łȂ��A���Q�����̖��ł��B�r�b�N������悤�ȏ�����(2)�ŁA�Ȃ��A�Ƃ����C�ɂ������܂��B(2)���ɂ������ǂ��̂ł����A(1)�̒i�K�ŋC�Â���ł��傤���H
(1)(i) 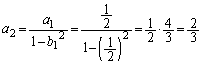 ......[��]
......[��] 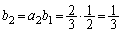 ......[��]
......[��]
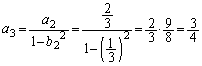 ......[��]
......[��]
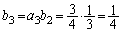 ......[��]
......[��](ii) 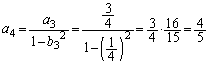
������A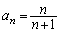 �C
�C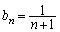 �Ɛ��肷�邱�Ƃ��ł��܂��B���肪���������Ƃ����w�I�A�[�@�ŏؖ����܂��B
�Ɛ��肷�邱�Ƃ��ł��܂��B���肪���������Ƃ����w�I�A�[�@�ŏؖ����܂��B (�T) 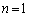 �̂Ƃ��A
�̂Ƃ��A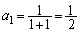 �C
�C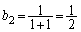 ���A����͐��藧���܂��B
���A����͐��藧���܂��B (�U) 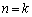 �̂Ƃ����肪���藧�A�܂�A
�̂Ƃ����肪���藧�A�܂�A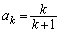 �C
�C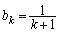 �Ɖ��肵�܂��B
�Ɖ��肵�܂��B ����āA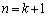 �̂Ƃ����������܂��B
�̂Ƃ����������܂��B (�T)�C(�U)���A���肪���������Ƃ��ؖ�����܂����B
(2)(i) 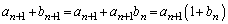
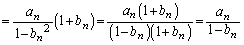 ......[��]
......[��](ii) 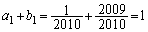
(i)���A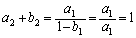
������A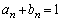 �Ɖ��肷��ƁA(i)���A
�Ɖ��肷��ƁA(i)���A ����āA�A�[�I�ɁA���ׂĂ̎��R��n�ɂ��āA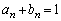 ......[��]
......[��] ���ӁD(2)(i)�́A������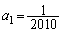 �C
�C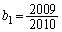 �łȂ��Ă��������܂��B(1)�̏�����
�łȂ��Ă��������܂��B(1)�̏�����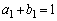 �����̂ŁA(1)�ł�
�����̂ŁA(1)�ł�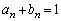 ���������܂��B(1)�ł́A����ɋC�Â��Ȃ��Ă��A�v�Z����₱�����Ƃ����킯�ł͂Ȃ��̂ŁA���Q�͂Ȃ��Ǝv���܂����A���Q������悤�ȓ����������邩���m��܂���B(1)�œ�q����悤�Ȃ�A(2)�����Ă݂�A�Ƃ����S���������悤�ɂ��܂��傤�B
���������܂��B(1)�ł́A����ɋC�Â��Ȃ��Ă��A�v�Z����₱�����Ƃ����킯�ł͂Ȃ��̂ŁA���Q�͂Ȃ��Ǝv���܂����A���Q������悤�ȓ����������邩���m��܂���B(1)�œ�q����悤�Ȃ�A(2)�����Ă݂�A�Ƃ����S���������悤�ɂ��܂��傤�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 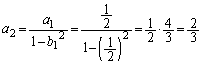 ......[��]
......[��]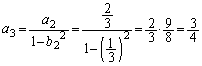 ......[��]
......[��]