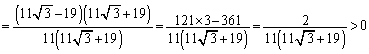���H�吔�w'10�N�O��[1]
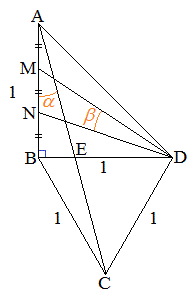
�l�p�`ABCD�͎��̏��������B
(i) 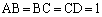
(ii) 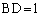 �C
�C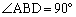
����AC�Ɛ���BD�̌�_��E�Ƃ���B����AB��3�������āA�_A�ɋ߂����_��M�Ƃ��A�_B�ɋ߂����_��N�Ƃ���B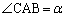 �C
�C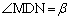 �Ƃ����Ƃ��A���̖₢�ɓ�����B
�Ƃ����Ƃ��A���̖₢�ɓ�����B
(1) �����̒����̔�̒l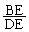 �����߂�B
�����߂�B (2) 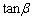 �̒l�����߂�B
�̒l�����߂�B (3) α��β �̑召�肹��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ���@��蕶��ǂ����ł͂��݂ǂ��낪�Ȃ��̂ł����A�E�}��`���Ό��ʂ����ǂ��Ȃ�͂��ł��B
���@��蕶��ǂ����ł͂��݂ǂ��낪�Ȃ��̂ł����A�E�}��`���Ό��ʂ����ǂ��Ȃ�͂��ł��B
(1) ����(i)�C(ii)���A��ABD��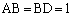 �ł��钼�p�ӎO�p�`�A��BCD��
�ł��钼�p�ӎO�p�`�A��BCD��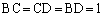 �ł��鐳�O�p�`�ł��B
�ł��鐳�O�p�`�ł��B �]���āA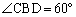 �C
�C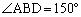 �ŁA��ABC��
�ŁA��ABC��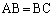 �ł���ӎO�p�`�B
�ł���ӎO�p�`�B
�� 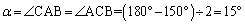
�� 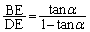 �@����@
�@����@ ���A
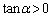 ���A
���A�@�ɑ������ƁA
(2) 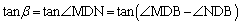
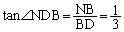 �C
�C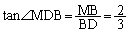
���A�ɑ������ƁA
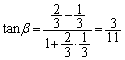 ......[��]
......[��]
(3) 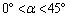 �C
�C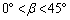 �Ȃ̂ŁAα�Cβ �̑召�W�ƁA
�Ȃ̂ŁAα�Cβ �̑召�W�ƁA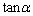 �C
�C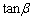 �̑召�W�͈�v���܂��B
�̑召�W�͈�v���܂��B �� 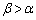 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 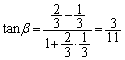 ......[��]
......[��]