�V���吔�w'10�N[2]
���̏���(�A)�`(�E)��������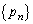 �ɂ��čl����B
�ɂ��čl����B
(�A) 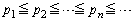 �ł���B
�ł���B (�C) 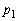 �C
�C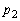 �C����C
�C����C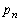 �C��� �͂ǂ�����R���ł���B
�C��� �͂ǂ�����R���ł���B (�E) 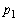 �C
�C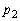 �C����C
�C����C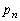 �C��� �̒��ɂ͂��ׂĂ̎��R��k������A���̌���k�ȏ�
�C��� �̒��ɂ͂��ׂĂ̎��R��k������A���̌���k�ȏ�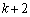 �ȉ��ł���B
�ȉ��ł���B ����(�A)�`(�E)�����A���ׂĂ̎��R��k�����傤��k����鐔��
��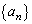 �Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) ����5�̐���ŁA����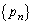 �̏��߂�5���ƂȂ蓾����̂����ׂċ�����B
�̏��߂�5���ƂȂ蓾����̂����ׂċ�����B (2) ����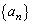 �̑�210��
�̑�210��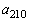 �̒l�����߂�B
�̒l�����߂�B (3) 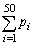 �̂Ƃ蓾��ŏ��̒l�����߂�B
�̂Ƃ蓾��ŏ��̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Q����̖��ł��B�e�Q�̌�����A�w�肳�ꂽ�����ǂ̌Q�ɑ����邩�A�Ƃ������Ƃ�s�����������ċ��߂܂��B�Ȃ��A���̌������Q�Ƃ��Ă��������B
(1) ����(�A)(�C)��萔��e���͏��������ɁA'1'�C'2'�C'3'�C����ƌ���܂��B����(�E)���A'1'��1�ȏ�3�ȉ��A'2'��2�ȏ�4�ȉ��A'3'��3�ȏ�5�ȉ������܂��B�ȉ��ŁA����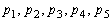 ��
��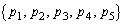 �ƕ\�����Ƃɂ��܂��B�W���̋L����p���ď����܂����A�W���̗v�f�������Â����Ă����Ǝv���Ă��������B
�ƕ\�����Ƃɂ��܂��B�W���̋L����p���ď����܂����A�W���̗v�f�������Â����Ă����Ǝv���Ă��������B 1��1�A2��2�A3��3�ȏ�ɂȂ�Ώ��߂�5���́A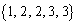 1��1�A2��3�A3��3�ȏ�ɂȂ�A
1��1�A2��3�A3��3�ȏ�ɂȂ�A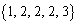 1��1�A2��4�ɂȂ�A
1��1�A2��4�ɂȂ�A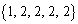 1��2�A2��2�A3��3�ȏ�ɂȂ�A
1��2�A2��2�A3��3�ȏ�ɂȂ�A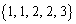 1��2�A2��3�ɂȂ�A
1��2�A2��3�ɂȂ�A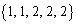 1��3�A2��2�ɂȂ�A
1��3�A2��2�ɂȂ�A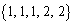
����őS���ł��B
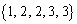 �C
�C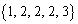 �C
�C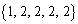 �C
�C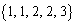 �C
�C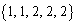 �C
�C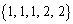 ......[��]
......[��] ���D�����̓��ĂƂ��ĒP�Ɍ��ʂ����������ł���A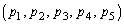 =
=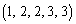 �C
�C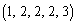 �C
�C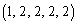 �C
�C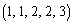 �C
�C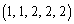 �C
�C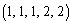 �Ə����̂��悢�悤�Ɏv���܂��B
�Ə����̂��悢�悤�Ɏv���܂��B
(2) k��k�����Ƃ�����k�Q�Ƃ���ƁA��k�Q�܂ł̍����́A
��210������k�Q�ɑ�����Ƃ��āA
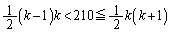 �@����@
�@����@�ƂȂ�͂��ł����A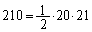 �Ȃ̂ŁA
�Ȃ̂ŁA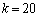 �ł��B
�ł��B
������A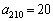 ......[��]
......[��]
(3) (1)�̌��ʂ����Ă���ƁA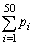 ���ŏ��ɂȂ�̂́A�������R�����ł����������Ƃ��ŁA'1'��3�A'2'��4�A'3'��5�A����A'k'��
���ŏ��ɂȂ�̂́A�������R�����ł����������Ƃ��ŁA'1'��3�A'2'��4�A'3'��5�A����A'k'��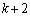 �����Ƃ��ł��Bk��
�����Ƃ��ł��Bk��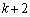 �����Ƃ�����k�Q�Ƃ���ƁA��k�Q�܂ł̍����́A
�����Ƃ�����k�Q�Ƃ���ƁA��k�Q�܂ł̍����́A �@�Ɠ��l�ɂ��āA��50������k�Q�ɑ�����Ƃ��āA
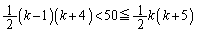 �@����A
�@����A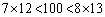
���A�A����k�́A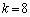 �ł��B
�ł��B
��8�Q�܂ł̍����́A �ł��B��52���܂łł���A'8'��10�����܂����A��50���܂łł́A'8'��8�������ƂɂȂ�܂��B����āA���̂Ƃ��A
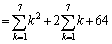
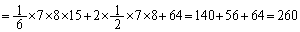 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B