��嗝�n���w'10�N�O��[4]
���a3�̋� �Ɣ��a1�̋�
�Ɣ��a1�̋� ���A���ڂ�����Ԃŋ�ԂɌŒ肳��Ă���B���a1�̋�S�����̏���(A)�C(B)���ɂ݂����Ȃ��瓮���B
���A���ڂ�����Ԃŋ�ԂɌŒ肳��Ă���B���a1�̋�S�����̏���(A)�C(B)���ɂ݂����Ȃ��瓮���B
(A) S��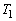 �̓����ɂ��邩
�̓����ɂ��邩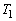 �ɓ��ڂ��Ă���B
�ɓ��ڂ��Ă���B (B) S�� �̊O���ɂ��邩
�̊O���ɂ��邩 �ɊO�ڂ��Ă���B
�ɊO�ڂ��Ă���B S�̒��S�����݂�����͈͂�D�Ƃ���Ƃ��A����D�̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��Ԑ}�`�̑̐ς̖��ł����A�����~�Ɠǂݑւ���A�̈ʒu�W���~�̈ʒu�W�Ƃ��čl���čs�����Ƃ��ł��܂��B����D���ǂ������}�`�ɂȂ�̂��A������x�̐����͕K�v�ł��傤�B
��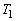 �̒��S�����_�A����ɓ��ڂ��鋅
�̒��S�����_�A����ɓ��ڂ��鋅 �̒��S�̍��W��
�̒��S�̍��W��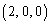 �Ƃ���悤�ȍ��W�n���Ƃ�܂��B�܂��A��
�Ƃ���悤�ȍ��W�n���Ƃ�܂��B�܂��A��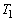 �̔��a��
�̔��a�� �C��
�C�� �̔��a��
�̔��a�� �Ƃ��܂��B
�Ƃ��܂��B
��S�̔��a��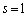 �Ƃ��A��S�̒��S�Ƌ�
�Ƃ��A��S�̒��S�Ƌ�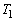 �̒��S�Ƃ̋�����
�̒��S�Ƃ̋�����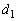 �Ƃ���ƁA����(A)���A���S�ԋ����͔��a�̍��ȉ�(��~�̈ʒu�W���Q��)�Ȃ̂ŁA
�Ƃ���ƁA����(A)���A���S�ԋ����͔��a�̍��ȉ�(��~�̈ʒu�W���Q��)�Ȃ̂ŁA
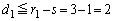 �@����@
�@����@ �̒��S�Ƃ̋�����
�̒��S�Ƃ̋����� �Ƃ���ƁA����(B)���A���S�ԋ����͔��a�̘a�ȏ�Ȃ̂ŁA
�Ƃ���ƁA����(B)���A���S�ԋ����͔��a�̘a�ȏ�Ȃ̂ŁA
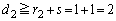 �@����A
�@����A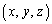 �Ƃ���ƁA�@���A
�Ƃ���ƁA�@���A
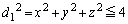 �@����B
�@����B
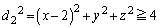 �@����C
�@����C
 ����āA����D���Axy����(
����āA����D���Axy����( )�Őؒf�����Ƃ��̒f��(�E�}���ΐF���F����)��x���̂܂��ɉ�]�������}�`�Ƃ��čl���邱�Ƃ��ł��A����D�̑̐ς���]�̂̑̐ςƂ��ċ��߂邱�Ƃ��ł��܂��B
)�Őؒf�����Ƃ��̒f��(�E�}���ΐF���F����)��x���̂܂��ɉ�]�������}�`�Ƃ��čl���邱�Ƃ��ł��A����D�̑̐ς���]�̂̑̐ςƂ��ċ��߂邱�Ƃ��ł��܂��B
�E�}�f�ʂ́A
 ����
���� 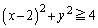
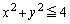 ����A
����A ����
���� 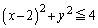 ��������(�͈�E�Ƃ��܂�)���������}�`�ł��B�͈�E�́A2�{�̋��E���͂ǂ�������a1�̉~�Ȃ̂�
��������(�͈�E�Ƃ��܂�)���������}�`�ł��B�͈�E�́A2�{�̋��E���͂ǂ�������a1�̉~�Ȃ̂� �Ɋւ��đΏ̂ł����āA�͈�E��x���̂܂��ɉ�]��������]�̂̑̐ς́A�~
�Ɋւ��đΏ̂ł����āA�͈�E��x���̂܂��ɉ�]��������]�̂̑̐ς́A�~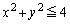 ��
��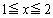 �̕�����x���̂܂��ɉ�]��������]�̂̑̐�
�̕�����x���̂܂��ɉ�]��������]�̂̑̐�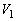 ��2�{�ł��B
��2�{�ł��B
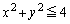 ���A
���A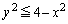
����D�̑̐�V�́A���a2�̋��̑̐ς���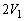 �������āA
�������āA
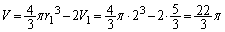 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B