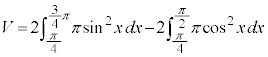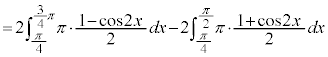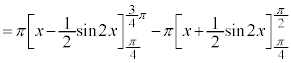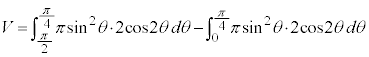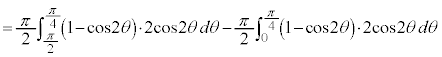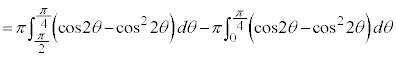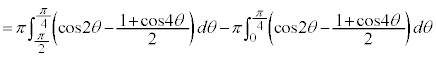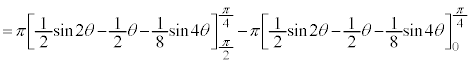x軸の回りの回転体 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、不定積分の公式、定積分と体積を参照してください。
曲線: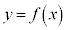 と直線:
と直線: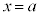 ,直線:
,直線: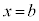 ,及びx軸で囲まれる図形をx軸の回りに1回転させてできる回転体の体積Vは、
,及びx軸で囲まれる図形をx軸の回りに1回転させてできる回転体の体積Vは、
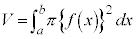
x軸に垂直な平面: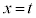 で切ったときの断面は、半径
で切ったときの断面は、半径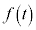 の円なので、断面積は:
の円なので、断面積は: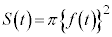
よって、回転体の体積Vは、
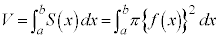
回転体の体積では、くりぬける部分ができる場合があるので注意してください。
くりぬける部分があるときには、外周の部分が作る回転体の体積から、くりぬける部分の体積を引く必要があります。
 例1. 2曲線、
例1. 2曲線、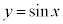 ,
,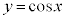 (
( )で囲まれる部分をx軸の回りに1回転させてできる回転体の体積を求める。
)で囲まれる部分をx軸の回りに1回転させてできる回転体の体積を求める。
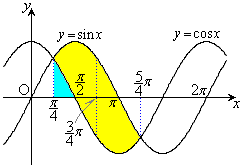
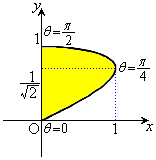
[解答] 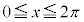 において、2曲線で囲まれる部分は、右図で黄色で塗られた部分。
において、2曲線で囲まれる部分は、右図で黄色で塗られた部分。
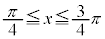 の部分を回転させたときの体積と、
の部分を回転させたときの体積と、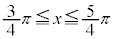 の部分を回転させたときの体積は等しいので、求める体積Vは、
の部分を回転させたときの体積は等しいので、求める体積Vは、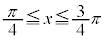 の部分を回転させたときの体積の2倍です。
の部分を回転させたときの体積の2倍です。
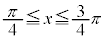 の部分を回転させると、外周部分は
の部分を回転させると、外周部分は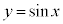 になりますが、
になりますが、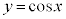 の
の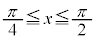 の部分とx軸に挟まれた部分(右図で水色に塗られている部分)については、くりぬかれていて回転体が存在しない部分なので、外周を回転させた体積から、くりぬかれている部分を引く必要があります。よって、
の部分とx軸に挟まれた部分(右図で水色に塗られている部分)については、くりぬかれていて回転体が存在しない部分なので、外周を回転させた体積から、くりぬかれている部分を引く必要があります。よって、
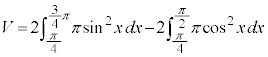
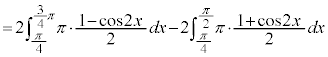
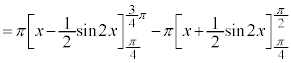
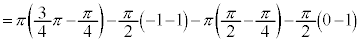
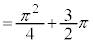 ......[答]
......[答]
 例2. 媒介変数表示された曲線:
例2. 媒介変数表示された曲線: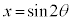 ,
,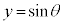 (
(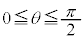 )で表された曲線とy軸で囲む部分を、x軸の回りに1回転させでできる回転体の体積を求める。
)で表された曲線とy軸で囲む部分を、x軸の回りに1回転させでできる回転体の体積を求める。
[解答] xは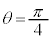 のときに最大値1をとり、θ が、
のときに最大値1をとり、θ が、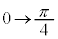 と変わるとき、xは
と変わるとき、xは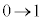 と変化し、yは
と変化し、yは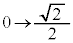 と変化します。
と変化します。
θ が、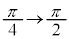 と変わるとき、xは
と変わるとき、xは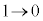 と変化し、yは
と変化し、yは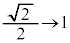 と変化します。
と変化します。
曲線のうち、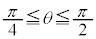 の部分が外周部分(
の部分が外周部分(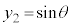 とします)であり、
とします)であり、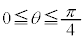 の部分が内周部分(
の部分が内周部分(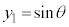 とします)になります。
とします)になります。
求める体積Vは、
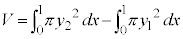
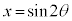 を微分して、
を微分して、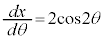 ,
,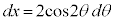 ,x:
,x: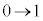 のとき、外周部分(
のとき、外周部分(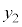 )においては、θ:
)においては、θ: 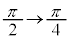 ,内周部分(
,内周部分(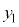 )においては、θ :
)においては、θ :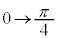
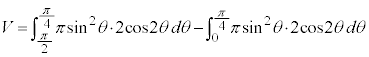
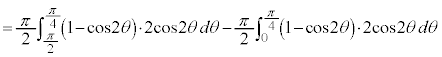
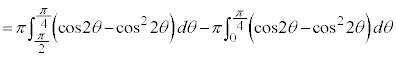
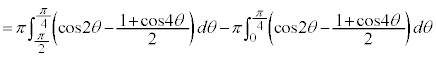
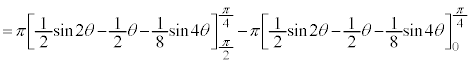
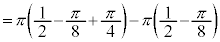
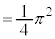 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。