九大数学'10年前期[2]
次のような競技を考える。競技者がサイコロを振る。もし、出た目が気に入ればその目を得点とする。そうでなければ、もう1回サイコロを振って、2つの目の合計を得点とすることができる。ただし、合計が7以上になった場合は得点は0点とする。この取り決めによって、2回目を振ると得点が下がることもあることに注意しよう。次の問いに答えよ。
(1) 競技者が常にサイコロを2回振るとすると、得点の期待値はいくらか。
(2) 競技者が最初の目が6のときだけ2回目を振らないとすると、得点の期待値はいくらか。
(3) 得点の期待値を最大にするためには、競技者は最初の目がどの範囲にあるときに2回目をふるとよいか。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 確率の基本問題です。全ての場合を書き出しても解答できるでしょう。
１回目に出る目をa，2回目に出る目をbとして、サイコロを2回振ったときに出る目を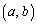
のように書くことにします。
(1) 2回サイコロを振って、2つの目の合計が7以上(得点は0点)にならないのは、以下の場合です。
得点2となるのが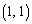
得点3となるのが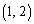
，
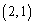
得点4となるのが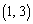
，
，
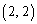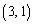
得点5となるのが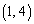
，
，
，
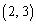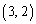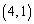
得点6となるのが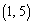
，
，
，
，
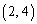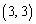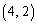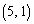2回の目の出方は各々
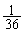なので、得点の期待値は、 
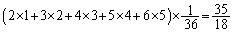......[答]
(2) 最初の目が6になる確率は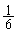
で、このとき得点は6です。得点の期待値は、 
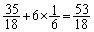......[答]
(3) (2)の場合に加えて最初の目が5のときにも2回目を振らないとすると、期待値は、(2)の場合よりも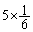
増えて、(1)の
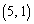の
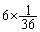減るので、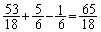
になります。 さらに最初の目が4のときにも2回目を振らないとすると、期待値は、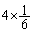
増えて、(1)の
，
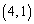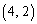の
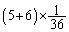減るので、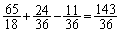
になります。
さらに最初の目が3のときにも2回目を振らないとすると、期待値は、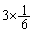
増えて、(1)の
，
，
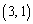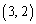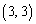の
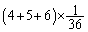減るので、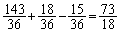
になります。
さらに最初の目が2のときにも2回目を振らないとすると、期待値は、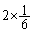
増えて、(1)の
，
，
，
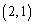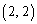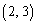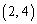の
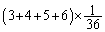減るので、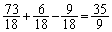
になります。
さらに最初の目が1のときにも2回目を振らないとすると、期待値は、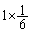
増えて、(1)の
，
，
，
，
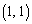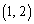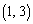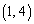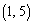の
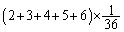減るので、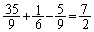
になります。このときには、最初の1回しか振らないので、
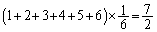としても期待値を求められます。
以上より、得点の期待値を最大にするためには、最初の目が1以上2以下の範囲 ......[答] のとき、2回目を振ればよいことになります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。