��吔�w'11�N�O��[5]
1����4�܂ł̐�����1�������ꂽ4���̃J�[�h������B����4���̃J�[�h�������ɕ��ׁA�ȉ��̑�����l����B
����F1����4�܂ł̐�����1�������ꂽ4�̋��������Ă���܂��瓯����2�̋������o���B���ɏ����ꂽ������i��j�Ȃ�Ai�̃J�[�h��j�̃J�[�h�����ւ���B���̌�A2�̋��͑܂ɖ߂��B
�͂��߂ɃJ�[�h�������珇��1�C2�C3�C4�ƕ��ׁA��̑����n��J��Ԃ�����̃J�[�h�ɂ��āA�ȉ��̖₢�ɓ�����B
(1) 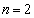 �̂Ƃ��A�J�[�h�������珇��1�C2�C3�C4�ƕ��Ԋm�������߂�B
�̂Ƃ��A�J�[�h�������珇��1�C2�C3�C4�ƕ��Ԋm�������߂�B (2)  �̂Ƃ��A�J�[�h�������珇��4�C3�C2�C1�ƕ��Ԋm�������߂�B
�̂Ƃ��A�J�[�h�������珇��4�C3�C2�C1�ƕ��Ԋm�������߂�B (3)  �̂Ƃ��A���[�̃J�[�h�̐�����1�ɂȂ�m�������߂�B
�̂Ƃ��A���[�̃J�[�h�̐�����1�ɂȂ�m�������߂�B (4) 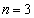 �̂Ƃ��A���[�̃J�[�h�̐����̊��Ғl�����߂�B
�̂Ƃ��A���[�̃J�[�h�̐����̊��Ғl�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(4)�ł́A���[��2������̂��A3������̂��A4������̂������m���ł��B
����1�C2�C3�C4�������ꂽ�����@�C�A�C�B�C�C�ƕ\�����Ƃɂ��܂��B
4�̋�����2�̋������o�����o�����́A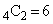 �ʂ肠��܂��B
�ʂ肠��܂��B
1��̑���ŁA����1�������ꂽ�J�[�h�����[�ɂ���̂́A�A�C�B�C�C��3�̒�����2�����o�����ꍇ�ŁA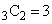 �ʂ肠���āA�����Ȃ�m����
�ʂ肠���āA�����Ȃ�m����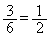 �ł��B
�ł��B
1��̑���ŁA����1�������ꂽ�J�[�h��������2�Ԗڂɂ���̂́A�@�ƇA�����o�����ꍇ�ŁA�����Ȃ�m���� �C���l�ɁA����1�������ꂽ�J�[�h��������3�Ԗڂɂ���m�����A4�Ԗڂɂ���m����
�C���l�ɁA����1�������ꂽ�J�[�h��������3�Ԗڂɂ���m�����A4�Ԗڂɂ���m����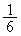 �ł��B
�ł��B
(1) 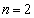 �̂Ƃ��A�J�[�h�������珇��1�C2�C3�C4�ƕ��Ԃ̂́A1��ڂɎ��o����2�̋��̑g�ݍ��킹��6�ʂ�̂�����ł����Ă��A2��ڂɎ��o����2�̋��̑g�ݍ��킹���A1��ڂɎ��o����2�̋��̑g�ݍ��킹�Ɠ����ɂȂ�ꍇ�ł��B
�̂Ƃ��A�J�[�h�������珇��1�C2�C3�C4�ƕ��Ԃ̂́A1��ڂɎ��o����2�̋��̑g�ݍ��킹��6�ʂ�̂�����ł����Ă��A2��ڂɎ��o����2�̋��̑g�ݍ��킹���A1��ڂɎ��o����2�̋��̑g�ݍ��킹�Ɠ����ɂȂ�ꍇ�ł��B ���̊m���́A ......[��]
......[��]
(2)  �̂Ƃ��A�J�[�h�������珇��4�C3�C2�C1�ƕ��Ԃ̂́A1��ڂɎ��o����2�̋��̑g�ݍ��킹���@�ƇC�ŁA2��ڂɎ��o����2�̋��̑g�ݍ��킹���A�ƇB�A���邢�́A1��ڂɎ��o����2�̋��̑g�ݍ��킹���A�ƇB�ŁA2��ڂɎ��o����2�̋��̑g�ݍ��킹���@�ƇC�ɂȂ�ꍇ�ł��B
�̂Ƃ��A�J�[�h�������珇��4�C3�C2�C1�ƕ��Ԃ̂́A1��ڂɎ��o����2�̋��̑g�ݍ��킹���@�ƇC�ŁA2��ڂɎ��o����2�̋��̑g�ݍ��킹���A�ƇB�A���邢�́A1��ڂɎ��o����2�̋��̑g�ݍ��킹���A�ƇB�ŁA2��ڂɎ��o����2�̋��̑g�ݍ��킹���@�ƇC�ɂȂ�ꍇ�ł��B ���̊m���́A ......[��]
......[��]
(3) ��L�̌����ɂ��A1��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���(�m�� )�Ƃ��A2��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���̂́A2��ڂ̑���ł��A�A�C�B�C�C��3�̒�����2�����o�����ꍇ�ŁA�����Ȃ�m���́A
)�Ƃ��A2��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���̂́A2��ڂ̑���ł��A�A�C�B�C�C��3�̒�����2�����o�����ꍇ�ŁA�����Ȃ�m���́A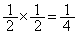 �ł��B
�ł��B 1��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ��Ȃ�(�m�� )�Ƃ��A2��̑���Ő���1�������ꂽ�J�[�h�����[�ɗ���̂́A2��ڂ̑���ŁA���[�ɂ���J�[�h�Ɠ��������̋��Ƈ@�����o���ꍇ�ŁA�����Ȃ�m���́A
)�Ƃ��A2��̑���Ő���1�������ꂽ�J�[�h�����[�ɗ���̂́A2��ڂ̑���ŁA���[�ɂ���J�[�h�Ɠ��������̋��Ƈ@�����o���ꍇ�ŁA�����Ȃ�m���́A �ł��B
�ł��B
���߂�m���́A ......[��]
......[��]
(4) (3)�̌��ʂ��A2��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���(�m��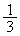 )�Ƃ��A3��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���̂́A3��ڂ̑���ŁA�A�C�B�C�C��3�̒�����2�����o�����ꍇ�ŁA�����Ȃ�m���́A
)�Ƃ��A3��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���̂́A3��ڂ̑���ŁA�A�C�B�C�C��3�̒�����2�����o�����ꍇ�ŁA�����Ȃ�m���́A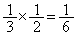 �ł��B
�ł��B 2��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ��Ȃ�(�m�� )�Ƃ��A3��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���̂́A3��ڂ̑���ŁA���[�ɂ���J�[�h�Ɠ��������̋��Ƈ@�����o���ꍇ�ŁA�����Ȃ�m���́A
)�Ƃ��A3��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���̂́A3��ڂ̑���ŁA���[�ɂ���J�[�h�Ɠ��������̋��Ƈ@�����o���ꍇ�ŁA�����Ȃ�m���́A �ł��B3��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���m���́A
�ł��B3��̑���Ő���1�������ꂽ�J�[�h�����[�ɂ���m���́A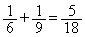 �ł��B
�ł��B
��L�̌������A1��̑����ɁA����1�������ꂽ�J�[�h��������2�ԖځA3�ԖځA4�Ԗڂɂ���m���͓�����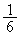 �ł��B�e��̑���O�ɁA����1�������ꂽ�J�[�h���ǂ̈ʒu�ɂ��Ă��A���̉�̑���ō�����2�ԖځA3�ԖځA4�Ԗڂɂ���m���͓������Ȃ�܂��B����2�C3�C4�̏����ꂽ�J�[�h�ɂ��Ă����l�̂��Ƃ������܂��B
�ł��B�e��̑���O�ɁA����1�������ꂽ�J�[�h���ǂ̈ʒu�ɂ��Ă��A���̉�̑���ō�����2�ԖځA3�ԖځA4�Ԗڂɂ���m���͓������Ȃ�܂��B����2�C3�C4�̏����ꂽ�J�[�h�ɂ��Ă����l�̂��Ƃ������܂��B
�]���āA3��̑���ŁA���[�ɐ���2�������ꂽ�J�[�h������m�����A����3�������ꂽ�J�[�h������m�����A����4�������ꂽ�J�[�h������m�����������Ȃ�A��������A �ƂȂ�܂��B����āA���߂����Ғl�́A 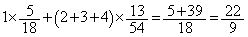 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B