�ꋴ�吔�w'08�N�O��[2]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
3��������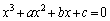 �͈قȂ�3�̉�p�Cq�Cr�����B����ɁA
�͈قȂ�3�̉�p�Cq�Cr�����B����ɁA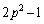 �C
�C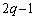 �C
�C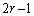 �������������̈قȂ�3�̉��ł���Ba�Cb�Cc�Cp�Cq�Cr�̑g�����ׂċ��߂�B
�������������̈قȂ�3�̉��ł���Ba�Cb�Cc�Cp�Cq�Cr�̑g�����ׂċ��߂�B
���@���낢��Ȃ��Ƃ��l�����܂��B�Ⴆ�A3����������x�ɁA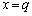 �C
�C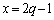 �������Ă݂�ƁA
�������Ă݂�ƁA
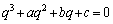 �C
�C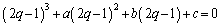
���ɁA���ƌW���̊W����A
�Ƃ��邱�Ƃ��l�����܂����A�����������Ȃ��Ă�͂��ɕ����܂���B
���������ӂ₳���ɁA���A�����������Ȃ�Ȃ��悤�ȁA��@��T�����ƂɂȂ�܂��B
����3����������3�̈قȂ�����A2�̕ʂ̌`�ŗ^�����Ă���A�Ƃ������Ƃ͂ǂ��������Ƃ��ƌ����ƁA
���Ƃ���ƁA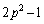 �C
�C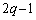 �C
�C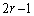 �����ꂼ��Aα�Cβ�Cγ �̂ǂꂩ���Ƃ������Ƃł��B
�����ꂼ��Aα�Cβ�Cγ �̂ǂꂩ���Ƃ������Ƃł��B
����Ȃ�A3�̈قȂ���̂̏����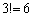 �ʂ�̏ꍇ����������A���������ӂ₳���ɁA���A���������������ɒ��ׂ邱�Ƃ��ł������ł��B
�ʂ�̏ꍇ����������A���������ӂ₳���ɁA���A���������������ɒ��ׂ邱�Ƃ��ł������ł��B
���̍ۂɁA��l�������̂��A��蕶��q��r�����ւ��ēǂ�ł��A���̈Ӗ��͕ς��Ȃ��A�Ƃ������Ƃł��B
�uq�Cr�̑Ώ̐����A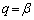 �C
�C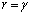 �����߂�g�ł���A
�����߂�g�ł���A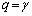 �C
�C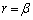 �����߂�g�ɂȂ�v�Ə����đ��v���Ǝv���܂����A�S�z�Ȃ�A�ꍇ��������Ƃ��ɁA
�����߂�g�ɂȂ�v�Ə����đ��v���Ǝv���܂����A�S�z�Ȃ�A�ꍇ��������Ƃ��ɁA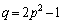 �̏ꍇ�ׂĂ����A
�̏ꍇ�ׂĂ����A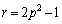 �̏ꍇ�ɂ��ẮA�u��ɒ��ׂ��ꍇ��q��r�Ɠ���ւ��邱�Ƃɂ��A���l�̌��ʂƂȂ�v�Ə����Ă����Ηǂ��ł��傤�B
�̏ꍇ�ɂ��ẮA�u��ɒ��ׂ��ꍇ��q��r�Ɠ���ւ��邱�Ƃɂ��A���l�̌��ʂƂȂ�v�Ə����Ă����Ηǂ��ł��傤�B
(1) 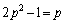 �̂Ƃ��A
�̂Ƃ��A (i) 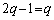 �C
�C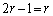 �̂Ƃ��A
�̂Ƃ��A 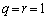 �ƂȂ�̂ŕs�K�B
�ƂȂ�̂ŕs�K�B(ii) 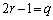 �C
�C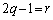 �̂Ƃ��A
�̂Ƃ��A �� 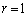
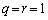 �ƂȂ�̂ŕs�K�B
�ƂȂ�̂ŕs�K�B
���ǁA(1)�͂��ׂĂ̏ꍇ�ɕs�K�ł��B
(2) 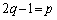 �@����@�@�̂Ƃ��A
�@����@�@�̂Ƃ��A (i) 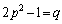 �C
�C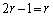 �̂Ƃ��A
�̂Ƃ��A �܂��A
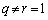 ���A
���A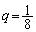
(ii) 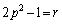 �C
�C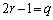 �̂Ƃ��A
�̂Ƃ��A �@�ɑ�����āA
�� 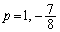
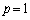 �̂Ƃ��A
�̂Ƃ��A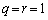 �ƂȂ邽�ߕs�K�B
�ƂȂ邽�ߕs�K�B
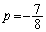 �̂Ƃ��A
�̂Ƃ��A
(3) 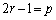 �̂Ƃ��A(2)�̏ꍇ��q�Cr�����ւ��邱�Ƃɂ��A
�̂Ƃ��A(2)�̏ꍇ��q�Cr�����ւ��邱�Ƃɂ��A a�Cb�Cc��(2)(i)�̏ꍇ�̒l�Ɠ����B
a�Cb�Cc��(2)(ii)�̏ꍇ�̒l�Ɠ����B
�ȏ���A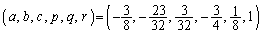 �C
�C
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B