一橋大数学'09年前期[4]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
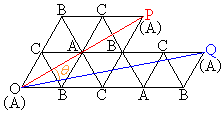
一辺の長さが2の正三角形ABCを平面上におく。△ABCを1つの辺に関して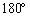
折り返すという操作を繰り返し行う。辺BCに関する折り返しを
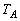，辺CAに関する折り返しを
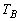，辺ABに関する折り返しを
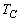とする。△ABCは、最初3点A，B，Cがそれぞれ平面上の3点O，
，
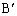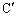の上に置かれているとする。
(1) 
，
，
，
，
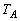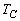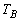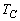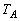の順に折り返し操作を施したときの頂点Aの移り先をPとする。また、
，
，
，
，
，
，
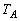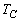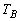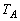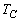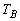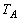の順に折り返し操作を施したときの頂点Aの移り先をQとする。
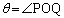とするとき、
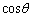の値を求めよ。 (2) 整数k，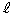
に対して、
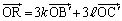により定められる点Rは、
，
，
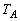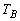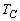の折り返し操作を組み合わせることにより、点Aの移り先になることを示せ。
解答 一橋大としては珍しいタイプの出題なので、一橋大受験生は面食らったかも知れませんが、理系の問題としてはしばしば見かけるパズル問題です。
，
，
，
，
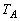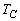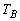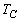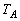の順に折り返し操作を施すと、AはOから右図のPに移ります。
，
，
，
，
，
，
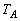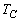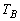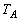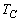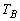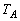の順に折り返し操作を施すと、Aは右図のQに移ります。
，
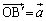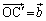
とおくと、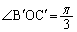
より、 より、
∴ 
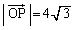
より、
∴ 
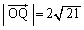
です。
なので、
∴ 
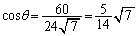......[答]
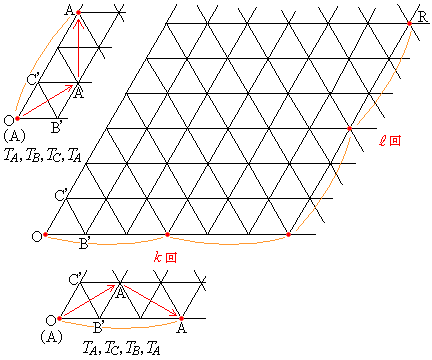(2) (1)に出てくる折り返し操作で、
，
，
，
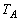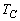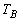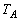という順に操作を行うとAは、となる点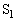
に移ります。この操作をk回繰り返せば、Aは、 となる点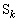
に移ります。同様に、
，
，
，
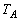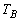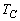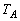という順に操作を行うとAは、 となる点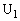
に移ります。この操作を
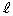回繰り返せば、Aは、 となる点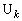
に移ります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
(1) 
，
，
は右図のような操作です。
では、操作前後のAの位置はBCに関して対称です。
，
，
，
という順の操作をk回行い、続けて、
，
，
，
という順の操作を
回行うことにより、Aは、点Rに移ります。従って、整数k，
に対して、
により定められる点Rは、
，
，
の折り返し操作を組み合わせることにより、点Aの移り先になります。
