�ꋴ�吔�w'11�N�O��[2]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�_O�𒆐S�Ƃ��锼�ar�̉~����ɁA2�_A�CB��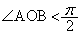 �ƂȂ�悤�ɂƂ�
�ƂȂ�悤�ɂƂ�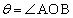 �Ƃ����B���̉~����ɓ_C���A����OC������AB�ƌ����悤�ɂƂ�A����AB��ɓ_D���Ƃ�B�܂��A�_P�͐���OA����A�_Q�͐���OB����A���ꂼ�ꓮ���Ƃ���B
�Ƃ����B���̉~����ɓ_C���A����OC������AB�ƌ����悤�ɂƂ�A����AB��ɓ_D���Ƃ�B�܂��A�_P�͐���OA����A�_Q�͐���OB����A���ꂼ�ꓮ���Ƃ���B
(1) 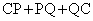 �̍ŏ��l��r��θ �ŕ\���B
�̍ŏ��l��r��θ �ŕ\���B (2) 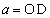 �Ƃ����B
�Ƃ����B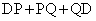 �̍ŏ��l��a��θ �ŕ\���B
�̍ŏ��l��a��θ �ŕ\���B (3) ����ɁA�_D������AB����Ƃ��� �̍ŏ��l��r��θ �ŕ\���B
�̍ŏ��l��r��θ �ŕ\���B
���@�����藝��]���藝�̓K�p�������Ԃ̂ł����A���܂������܂���B���W�ݒ肵�Ă݂Ă����`�������܂���B�ł����A�~����Ɉʒu����_�́A���a�Ɋւ���Ώ̓_�́A�~����ɗ���A�Ƃ������ƂɋC�Â��Ηe�Ղɉ������܂��B
 (1) ����OA�Ɋւ���C�̑Ώ̓_��E�C����OB�Ɋւ���C�̑Ώ̓_��F�Ƃ���ƁAE�CF�́A�_O�𒆐S�Ƃ��锼�ar�̉~����̓_�ł��B�܂��A
(1) ����OA�Ɋւ���C�̑Ώ̓_��E�C����OB�Ɋւ���C�̑Ώ̓_��F�Ƃ���ƁAE�CF�́A�_O�𒆐S�Ƃ��锼�ar�̉~����̓_�ł��B�܂��A �C
�C �C
�C �C
�C �ł��B
�ł��B �@����@
�@����@�ƂȂ�܂����A����EF�ƁA����OA�C����OB�Ƃ̌�_��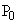 �C
�C �Ƃ���ƁA
�Ƃ���ƁA �C
�C ���A
���A  �@����A
�@����A�@�C�A���A
����́A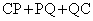 �̍ŏ��l��EF�ł��邱�Ƃ������Ă��܂��B
�̍ŏ��l��EF�ł��邱�Ƃ������Ă��܂��B 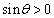 ���A
���A
����āA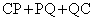 �̍ŏ��l��
�̍ŏ��l��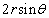 ......[��]
......[��]
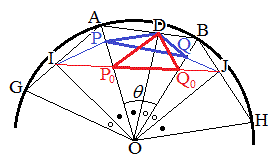 (2) ����OA�Ɋւ���B�̑Ώ̓_��G�C����OB�Ɋւ���A�̑Ώ̓_��H�Ƃ���ƁAG�CH�́A�_O�𒆐S�Ƃ��锼�ar�̉~����̓_�ł��B����AB��̓_D�̒���OA�Ɋւ���Ώ̓_I�͐���AG��̓_�ł��BD�̒���OB�Ɋւ���Ώ̓_J�͐���BH��̓_�ł��B
(2) ����OA�Ɋւ���B�̑Ώ̓_��G�C����OB�Ɋւ���A�̑Ώ̓_��H�Ƃ���ƁAG�CH�́A�_O�𒆐S�Ƃ��锼�ar�̉~����̓_�ł��B����AB��̓_D�̒���OA�Ɋւ���Ώ̓_I�͐���AG��̓_�ł��BD�̒���OB�Ɋւ���Ώ̓_J�͐���BH��̓_�ł��B �@����B
�@����B�ƂȂ�܂����A����IJ�ƁA����OA�C����OB�Ƃ̌�_�� �C
�C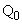 �Ƃ���ƁA
�Ƃ���ƁA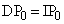 �C
�C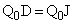 ���A
���A 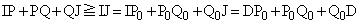 �@����C
�@����C�B�C�C���A
����́A �̍ŏ��l��IJ�ł��邱�Ƃ������Ă��܂��B
�̍ŏ��l��IJ�ł��邱�Ƃ������Ă��܂��B �]���藝���A
 �@(�{�p�̌����𗘗p)
�@(�{�p�̌����𗘗p)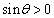 ���A
���A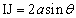 ����āA
����āA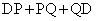 �̍ŏ��l��
�̍ŏ��l�� ......[��]
......[��]
(3) �_O�������AB�ɐ���OK (K�͐���AB�̒��_�ł�)�����낵�A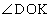 �̑傫����φ (
�̑傫����φ ( )�Ƃ���ƁA
)�Ƃ���ƁA �_D������AB����Ƃ���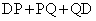 �̍ŏ��l�́A
�̍ŏ��l�́A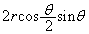 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B