�s��������@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����̒萔a�Cb�Cc (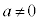 �C
�C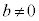 )�ɂ��āA
)�ɂ��āA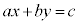 ���������̑g
���������̑g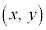 �����߂��肪����܂��B�����1���s��������ƌ����܂��B
�����߂��肪����܂��B�����1���s��������ƌ����܂��B
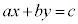 ��xy���ʏ�Œ�����\���܂����A1���s����������������̑g�����߂邱�Ƃ́A������̊i�q�_�����߂邱�ƂɑΉ����܂��B
��xy���ʏ�Œ�����\���܂����A1���s����������������̑g�����߂邱�Ƃ́A������̊i�q�_�����߂邱�ƂɑΉ����܂��B
a�Cb���݂��ɑf�Ȑ����Ƃ��܂��B
�s��������F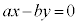 �@����@
�@����@
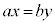 ���Ax��b�̔{���ŁA����k��p���āA
���Ax��b�̔{���ŁA����k��p���āA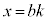 �Ƃ����܂��B
�Ƃ����܂��B
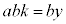 ���A
���A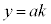
�������ć@�̐������́A����k��p���āA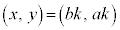
�s��������F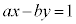 �@����A
�@����A
���炩�̕��@�œ����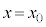 �C
�C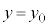 �����������Ƃ��܂��B
�����������Ƃ��܂��B
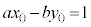 �@����B
�@����B
�A�|�B���A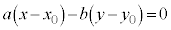
�@�̉��Ɠ��l�ɂ��āA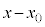 ��b�̔{���ŁA����k��p���āA
��b�̔{���ŁA����k��p���āA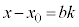 �Ƃ����܂��B
�Ƃ����܂��B
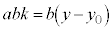 ���A
���A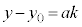
�A�̐������́A����k��p���āA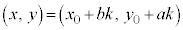
�s��������F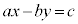 �@����C
�@����C
�C��c��1�Ƃ����s��������F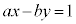 �̓������
�̓������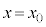 �C
�C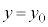 ���Ƃ��܂��B
���Ƃ��܂��B
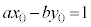
���ӂ�c�������āA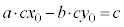 �@����D
�@����D
�C�|�D���A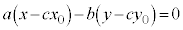
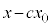 ��b�̔{���ŁA����k��p���āA
��b�̔{���ŁA����k��p���āA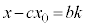 �Ƃ����܂��B
�Ƃ����܂��B
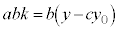 ���A
���A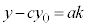
�C�̐������́A����k��p���āA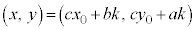
�s��������A�C�s��������C�ł́A�܂��A��������ǂ�����Č����邩�����ɂȂ�܂��B
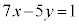
�̂悤�ȊȒP�ȕs��������ł���A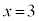 �C
�C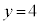 �Ƃ���������܂��B�ł����A
�Ƃ���������܂��B�ł����A
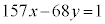 �@����@
�@����@
�̂悤�ȏꍇ�A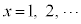 �Ƒ�����Ă����Ă��ȒP�ɂ͌�����܂���B
�Ƒ�����Ă����Ă��ȒP�ɂ͌�����܂���B
���̂Ƃ��ɗL���ȕ��@���AEuclid�̌ݏ��@�ł��B
157��68��2���܂�21�C�܂�A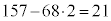 �@����A
�@����A
68��21��3���܂�5�C�܂�A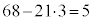 �@����B
�@����B
21��5��4���܂�1�C�܂�A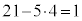 �@����C
�@����C
�ݏ��@���J��Ԃ��Ă��܂肪1 (157��68�̍ő����1�C�܂�A157��68���݂��ɑf�A�Ƃ������Ƃ��Ӗ����Ă��܂�)�ɂȂ����Ƃ���ŁA�B����o�����āA�܂��A�C��5�̂Ƃ���ɒ��O�̇B�������܂��B
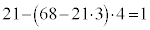
��������ƁA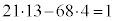 �@����D
�@����D
����ɇD��21�̂Ƃ���ɇ@�������܂��B
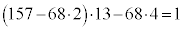
��������ƁA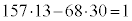
���̕s��������@�Ɣ�r����ƁA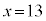 �C
�C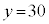 ���A�@�̓������^���邱�Ƃ��킩��܂��B
���A�@�̓������^���邱�Ƃ��킩��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B