��ϕ��ƕs�����@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
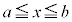 �ɂ����āA
�ɂ����āA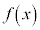 �C
�C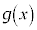 ���ϕ��\�ŁA���͈̔͂ɂ����āA
���ϕ��\�ŁA���͈̔͂ɂ����āA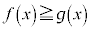 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A
�@�@�@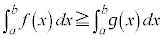
�s�����̓����́A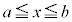 �ɂ�����C�ӂ�x�ɂ��āA
�ɂ�����C�ӂ�x�ɂ��āA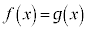 �ł���Ƃ��Ɍ��萬������B
�ł���Ƃ��Ɍ��萬������B
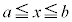 �ɂ����āA
�ɂ����āA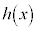 ���ϕ��\�ŁA
���ϕ��\�ŁA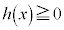 �Ƃ���Ƃ��A�敪���ϖ@�̋c�_���A��ϕ�
�Ƃ���Ƃ��A�敪���ϖ@�̋c�_���A��ϕ�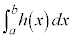 �́A�Ȑ�
�́A�Ȑ�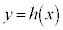 �ƁAx���A����
�ƁAx���A����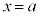 �C����
�C����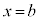 �ɂ���Ĉ͂܂�镔���̖ʐ�(���̒l�ɂ͂Ȃ�܂���)��\���܂��B
�ɂ���Ĉ͂܂�镔���̖ʐ�(���̒l�ɂ͂Ȃ�܂���)��\���܂��B
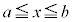 �ɂ�����C�ӂ�x�ɂ��āA
�ɂ�����C�ӂ�x�ɂ��āA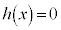 �ł���A
�ł���A
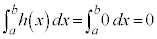 �@����@
�@����@
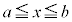 �Ɋ܂܂�邠����
�Ɋ܂܂�邠����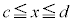 �ɂ����āA
�ɂ����āA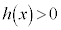 �ł���A���炩�ɁA
�ł���A���炩�ɁA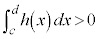 �ł��B
�ł��B
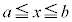 ���̎c���Ԃɂ����Ă��A���炩�ɁA
���̎c���Ԃɂ����Ă��A���炩�ɁA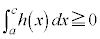 �C
�C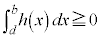 �ł��B����āA
�ł��B����āA
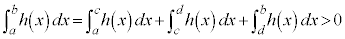
�@�ƍ��킹�āA
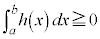 �@����A
�@����A
�s�����̓����́A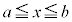 �ɂ�����C�ӂ�x�ɂ��āA
�ɂ�����C�ӂ�x�ɂ��āA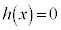 �ł���Ƃ��Ɍ��萬�����܂��B
�ł���Ƃ��Ɍ��萬�����܂��B
�����ŁA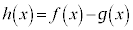 �Ƃ����ƁA
�Ƃ����ƁA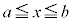 �ɂ����āA
�ɂ����āA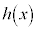 �͐ϕ��\�ŁA
�͐ϕ��\�ŁA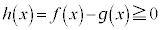 �ł��B
�ł��B
����āA�A�ɂ��A
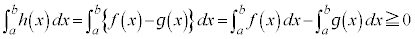
�ł���A�s�����̓����́A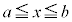 �ɂ�����C�ӂ�x�ɂ��āA
�ɂ�����C�ӂ�x�ɂ��āA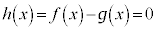 �C�܂�A
�C�܂�A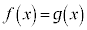 �ł���Ƃ��Ɍ��萬�����܂��B
�ł���Ƃ��Ɍ��萬�����܂��B
�� 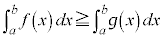
�s�����̓����́A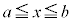 �ɂ�����C�ӂ�x�ɂ��āA
�ɂ�����C�ӂ�x�ɂ��āA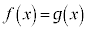 �ł���Ƃ��Ɍ��萬�����܂��B
�ł���Ƃ��Ɍ��萬�����܂��B
(�ؖ��I)
��L�̏ؖ��Ɠ��l�Ȃ��Ƃ��l�����������܂��B
��1�D�@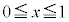 �ɂ����āA�ϕ��\��2��ȏ�����\�Ȋ�
�ɂ����āA�ϕ��\��2��ȏ�����\�Ȋ�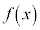 ������Ƃ��A
������Ƃ��A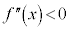 ����
���� 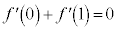 ����
���� 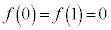 �ł���A
�ł���A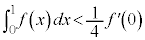 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B
[��]�@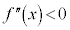 ���A
���A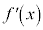 �͒P�������ŁA
�͒P�������ŁA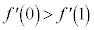 �ł��B�܂��A
�ł��B�܂��A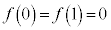 ���A
���A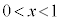 �ɂ����āA
�ɂ����āA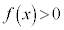 �ł��B
�ł��B
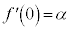 �Ƃ����ƁA
�Ƃ����ƁA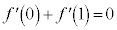 ���A
���A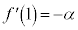 �C�܂��A
�C�܂��A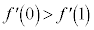 ���A
���A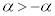
�� 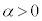
�܂��A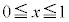 �ɂ����āA
�ɂ����āA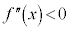 ���A�Ȑ�
���A�Ȑ�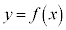 �͏�ɓʂŁA�ڐ����牺���ɗ��܂��B�@����@
�͏�ɓʂŁA�ڐ����牺���ɗ��܂��B�@����@
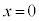 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A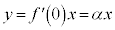 �@����A
�@����A
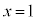 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A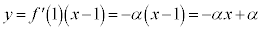 �@����B
�@����B
�A�C�B��A������ƁA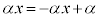
�� 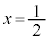
����āA2�ڐ��A�C�B�̌�_�́A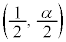 �ł��B
�ł��B
�@���A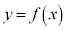 ��x���ň͂ޕ����̖ʐς́A2�����A�C�B��x���ň͂ޕ���(���1�C����
��x���ň͂ޕ����̖ʐς́A2�����A�C�B��x���ň͂ޕ���(���1�C����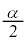 �̎O�p�`)�̖ʐ�
�̎O�p�`)�̖ʐ�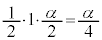 �����������Ȃ�܂��B����āA
�����������Ȃ�܂��B����āA
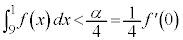
��L�̌��ʁF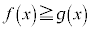 ��
�� 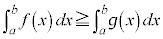 ���g����������܂��B
���g����������܂��B
��2�D�@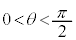 �̂Ƃ��A
�̂Ƃ��A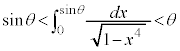 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B
[��] �s�������ӂ̒�ϕ��͌v�Z�ł��Ȃ��̂ŁA��ϕ��̌v�Z�����Ȃ��Ŏ������Ƃ��l���܂��B
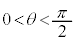 �̂Ƃ��A
�̂Ƃ��A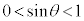 �ł��B
�ł��B
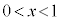 �ɂ����āA
�ɂ����āA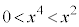 ���A
���A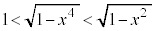 �ł���A
�ł���A
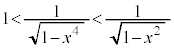 ���������܂��B����āA
���������܂��B����āA
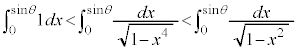 �@����@�@(��ϕ����Ɋւ���s�����ɓ���������Ȃ��̂ŁA��ϕ��̕s�����ɂ�����������Ȃ����Ƃɒ���)
�@����@�@(��ϕ����Ɋւ���s�����ɓ���������Ȃ��̂ŁA��ϕ��̕s�����ɂ�����������Ȃ����Ƃɒ���)
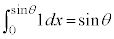
�@�E�ӂ̒�ϕ��́A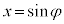 �Ƃ����ƁA
�Ƃ����ƁA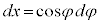 �Cx�F
�Cx�F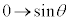 �̂Ƃ��Aφ�F
�̂Ƃ��Aφ�F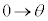
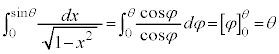 �@(�u���ϕ�(����2)���Q��)
�@(�u���ϕ�(����2)���Q��)
�@�ɑ�����āA
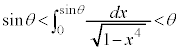
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 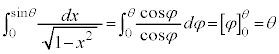 �@(�u���ϕ�(����2)���Q��)
�@(�u���ϕ�(����2)���Q��)