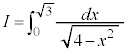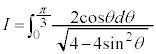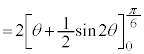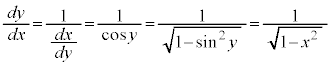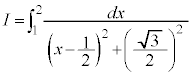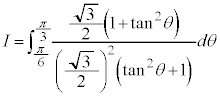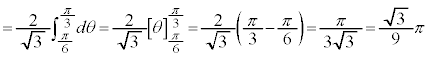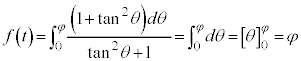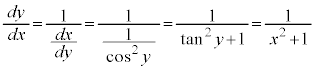置換積分(その2) 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目は、不定積分の公式、置換積分を参照してください。
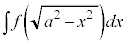 の場合では、
の場合では、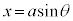 とおくと、うまくいくことがあります。
とおくと、うまくいくことがあります。
例1.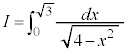
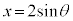 とおくと、
とおくと、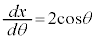 ,
,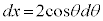
x: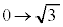 のとき、θ :
のとき、θ :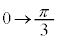
∴ 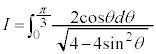
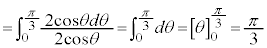
例2.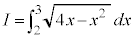
根号内を平方完成します。
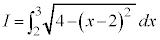
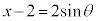 とおくと、
とおくと、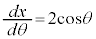 ,
,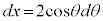
x: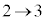 のとき、θ?:
のとき、θ?: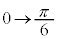
∴ 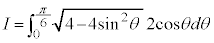
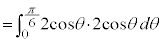
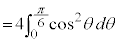
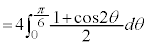
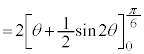
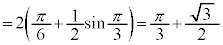
 [別解] 置換積分の定石通りやれば上記の通りなのですが、入試会場では時間の制約もあるので、以下のような方針で答案を作成してください。
[別解] 置換積分の定石通りやれば上記の通りなのですが、入試会場では時間の制約もあるので、以下のような方針で答案を作成してください。
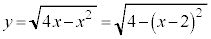 の両辺を2乗して整理すると、
の両辺を2乗して整理すると、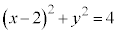 となるので、被積分関数は
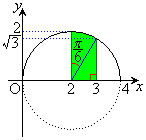
となるので、被積分関数は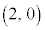 を中心とする円のx軸から上側の部分であって、積分は、この円の
を中心とする円のx軸から上側の部分であって、積分は、この円の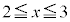 の部分とx軸の間に挟まれた領域(右図緑色の部分)の面積に相当します。
の部分とx軸の間に挟まれた領域(右図緑色の部分)の面積に相当します。
右図で、半径2,中心角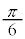 の扇形の面積と、底辺1,高さ
の扇形の面積と、底辺1,高さ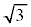 の直角三角形の面積を加えることにより、
の直角三角形の面積を加えることにより、
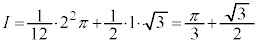
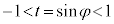 ,
,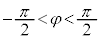 として、
として、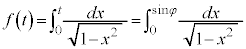 を考えます。
を考えます。
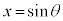 とおくと、
とおくと、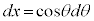 ,x:
,x: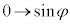 のとき、θ :
のとき、θ :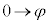 より、
より、
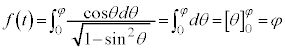
となりますが、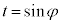 なので、
なので、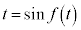
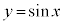 ,
,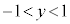 ,
,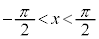 であれば、xとyの関係は1対1なので、
であれば、xとyの関係は1対1なので、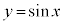 の逆関数を考えることができます。
の逆関数を考えることができます。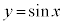 のとき、
のとき、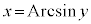 と書くことにすると、
と書くことにすると、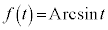 と書くことができます。
と書くことができます。
従って、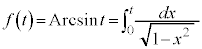 ,
,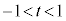 ,
,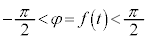 として、
として、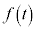 は正弦関数の逆関数になっていることがわかります。
は正弦関数の逆関数になっていることがわかります。
つまり、正弦がtになるときの角が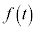 です。
です。
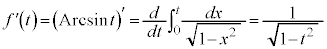 ,つまり、
,つまり、
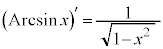
です。
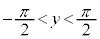 では、
では、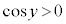 なので、
なので、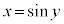 のとき、逆関数の微分法により、
のとき、逆関数の微分法により、
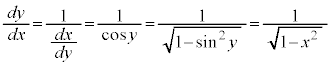
となることに注意してください。
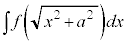 の場合は、
の場合は、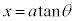 とおくと、うまくいくことがあります。
とおくと、うまくいくことがあります。
例3.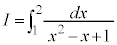
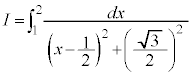
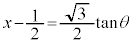 とおくと、
とおくと、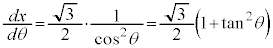 ,
,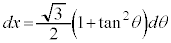
x: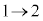 のとき、θ :
のとき、θ :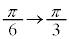 より、
より、
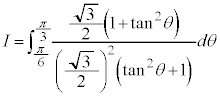
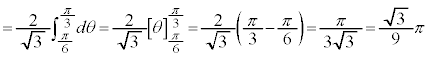
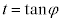 ,
,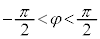 として、
として、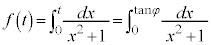 を考えます。
を考えます。
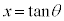 とおくと、
とおくと、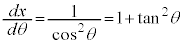 ,
,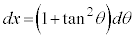
x: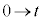 のとき、θ :
のとき、θ :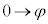 より、
より、
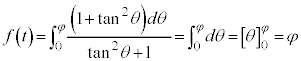
となりますが、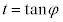 なので、
なので、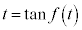
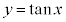 ,
,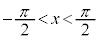 であれば、xとyの関係は1対1なので、
であれば、xとyの関係は1対1なので、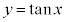 の逆関数を考えることができます。
の逆関数を考えることができます。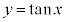 のとき、
のとき、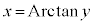 と書くことにすると、
と書くことにすると、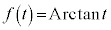 と書くことができます。
と書くことができます。
従って、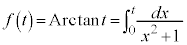 ,
,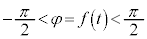 として、
として、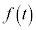 は正接関数の逆関数になっていることがわかります。
は正接関数の逆関数になっていることがわかります。
つまり、正接がtになるときの角が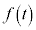 です。
です。
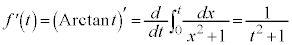 ,つまり、
,つまり、
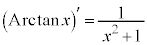
です。
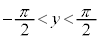 ,
,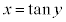 のとき、逆関数の微分法により、
のとき、逆関数の微分法により、
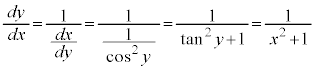
となることに注意してください。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。