逆関数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
関数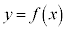 により、1つのxの値に対して1つのyの値が対応するとき、関数
により、1つのxの値に対して1つのyの値が対応するとき、関数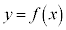 に対して、逆にyの値を1つ決めたときに、yに対応するxの値がただ1つ定まるとき、xをyの関数とみて、逆関数と言います。
に対して、逆にyの値を1つ決めたときに、yに対応するxの値がただ1つ定まるとき、xをyの関数とみて、逆関数と言います。
高校の範囲では、xとyが1対1に対応する必要があります。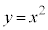 では、異なるxの2つの値に対して1つのyの値が対応することがある(
では、異なるxの2つの値に対して1つのyの値が対応することがある(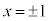 に対して
に対して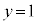 が対応する)ので、逆関数を考えることができません。xの定義域を
が対応する)ので、逆関数を考えることができません。xの定義域を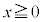 に限れば、
に限れば、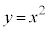 の逆関数
の逆関数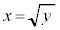 を考えることができます。
を考えることができます。
関数と言うときに、普通、変数をx,関数の値をyで表すので、そうした書き方をする場合には、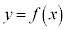 の逆関数を
の逆関数を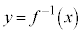 と書きます(
と書きます(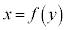 をyについて解き直して
をyについて解き直して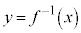 とする。xとyが入れ替わっていることに注意)。
とする。xとyが入れ替わっていることに注意)。
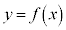 ⇔
⇔ 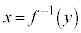 です。このとき、
です。このとき、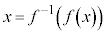 となります(逆関数の逆関数で元に戻る)。
となります(逆関数の逆関数で元に戻る)。
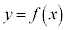 のグラフと
のグラフと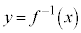 のグラフとは、xとyが入れ替わるので、直線
のグラフとは、xとyが入れ替わるので、直線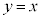 に関して対称になります。
に関して対称になります。
導関数については、逆関数の微分法を参照してください。
例.逆関数の例
(1) 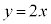 と、
と、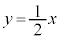
(2) 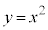 (
(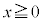 )と、
)と、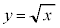
(3) 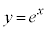 と、
と、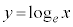
(4) 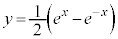 (
(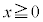 )と、
)と、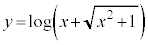
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。