慶大理工数学'08年[B1]
nは正の整数とする。
(1) 
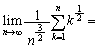ヘ である。 以下でp，q，rは正の実数とする。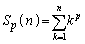
とおく。
(2) すべてのnに対し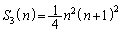
であることを証明しなさい。 (3) 極限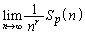
が0でない有限の値となるのは、rとpの間に関係式
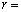ホ が成り立つときのみである。そのときの極限値をpを用いてあらわせば マ である。さらに
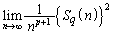が0でない有限の値となるのは、pとqの間に関係式
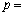ミ が成り立つときに限る。 (4) すべてのnに対し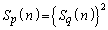
が成り立つための必要十分条件は、
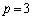かつ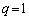
であることを証明しなさい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 2008年は、江戸時代の和算研究家、関孝和の没後300年に当たります。1712年、関孝和の死後出版された「括要算法」という本に、本問の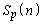
をnの式で表したときの係数の記述があるのだそうです。1713年に出版された、スイス人数学者、ヤコブ・ベルヌーイの確率論の本には、
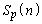の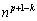
(
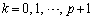)の係数は、
(
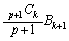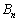はベルヌーイ数と言い、
，
，
，
，
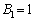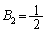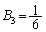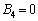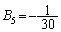，･･･)と表されると書いてあり、これと実質的に同じ結果が「括要算法」にも載っているそうです。全く同時期に、鎖国をしていた日本とヨーロッパとで同じ結果を出していたのが凄いと思いますが、本問は関孝和没後300年にちなんだ問題なのでしょうか。
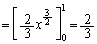......[答]
(2) 
・
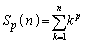
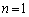のとき、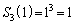
よって、成り立ちます。
・
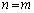のとき、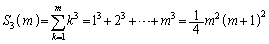
が成り立つと仮定します。 両辺に、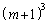
を加えると、 よって、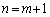
のときも成り立ちます。 以上より、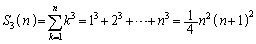
が成り立ちます。 (証明終)
(3) 
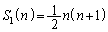はnの2次式、
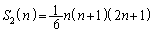はnの3次式、
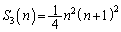はnの4次式なので、
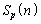はnの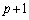
次式で、最高次の係数は
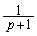だろうということは予測がつきます。これで、(ホ)は
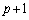，(マ)は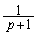
と埋めることができます。 (ホ) ここでは、(1)と同様の計算をして確かめておくことにします。
これは、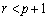
のときに発散し、
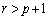のときに0に収束します。
極限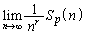
が0でない有限の値となるのは、
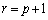......[答] のときで、 (マ) その極限値は、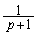
......[答] (ミ)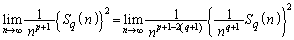 
これは、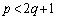
のときに発散し、
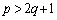のときに0に収束します。
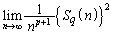が0でない有限の値となるのは、
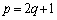......[答] のときです。pが自然数であれば、連続p整数の積のn項の和：
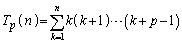を考えることもできます。 
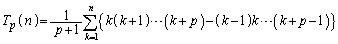(Σの中を差の形にした)
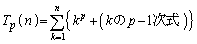と見ると、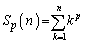
をnの多項式で表すとき、最高次の項は、
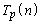の最高次の項
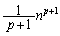に一致することがわかります。
ここからも、この(3)を考えることができます。
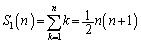と(2)により、
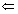は示されています。
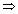を示します。
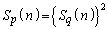のとき、(3)より、
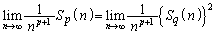は有限な値となります。は、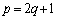
のときに限り0以外の有限な値に収束して、 ∴ 
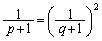よって、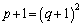
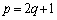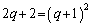
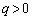より、
より、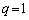
，
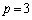
以上より、すべてのnに対し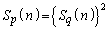
が成り立つための必要十分条件は、
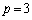かつ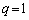
です。 (証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
が成り立つ” 
“
かつ
”
