�c��㐔�w'10�N[2]
�ȉ��̕��͂̋ɓK�Ȑ��܂��͎������ĕ��͂����������Ȃ����B�܂��A�ݖ�(2)(ii)�ɓ����Ȃ����B
���W���ʂɂ�����A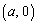 (������
(������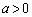 )��x����̒�_�Ƃ��A�Ȑ�C��o�Ȑ�
)��x����̒�_�Ƃ��A�Ȑ�C��o�Ȑ�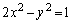 ��
��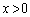 �ɑ��镔���Ƃ���B�Ȑ�C��̓_Q�ɑ��A�_P������
�ɑ��镔���Ƃ���B�Ȑ�C��̓_Q�ɑ��A�_P������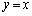 ����Ƃ���
����Ƃ���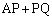 �̍ŏ��l��
�̍ŏ��l��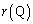 �ƒ�`����B
�ƒ�`����B
(1) Q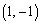 �ɑ���
�ɑ���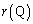 ��a�̎��ŕ\����
��a�̎��ŕ\����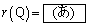 �ł���AQ
�ł���AQ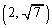 �ɑ��Ă�
�ɑ��Ă�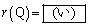 �ł���B
�ł���B (2) �����Q���Ȑ�C����Ƃ���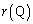 �̍ŏ��l���l����B
�̍ŏ��l���l����B (i) 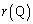 ��Q
��Q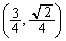 �ɂ����čŏ��l���Ƃ�̂�
�ɂ����čŏ��l���Ƃ�̂�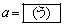 �̂Ƃ��ł���AQ
�̂Ƃ��ł���AQ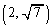 �ɂ����čŏ��l���Ƃ�̂�
�ɂ����čŏ��l���Ƃ�̂�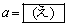 �̂Ƃ��ł���B
�̂Ƃ��ł���B (ii) 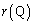 ��Q
��Q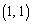 �ɂ����čŏ��l���Ƃ�悤��a�͈̔͂����߂Ȃ����B
�ɂ����čŏ��l���Ƃ�悤��a�͈̔͂����߂Ȃ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���������Ȃ�e�Ղɂ킩���Ă��܂��̂ŁA��[���Ƃ��Ă͓��Ƃ͌����܂��A���ɁA������Ƙ_�q����A�Ƃ������ƂɂȂ�Ɩ��Ȗ��ł��B�Ȃ��A2�����̍ő�E�ŏ����Q�Ƃ��Ă��������B
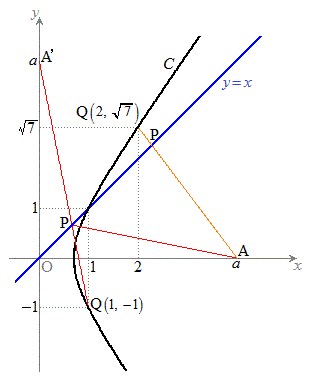 �o�Ȑ�C�F
�o�Ȑ�C�F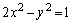 �ƒ���
�ƒ���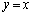 ��}������ƉE�}�̂悤�ɂȂ�܂��B
��}������ƉE�}�̂悤�ɂȂ�܂��B
������A������ƁA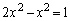 ���A
���A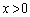 �ɂ����ẮA
�ɂ����ẮA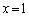 �C
�C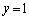
�o�Ȑ�C�ƒ����̌�_��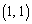 �ł��B
�ł��B
(1)(��) Q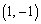 �ɑ��āA
�ɑ��āA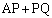 ���ŏ��Ƃ���A����
���ŏ��Ƃ���A����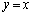 ��̓_P�́AA��
��̓_P�́AA��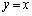 �Ɋւ���Ώ̓_
�Ɋւ���Ώ̓_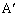
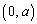 ��Q�����Ԓ����ƒ���
��Q�����Ԓ����ƒ���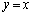 �Ƃ̌�_�ł��B
�Ƃ̌�_�ł��B ����ȊO�̒���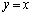 ��̓_
��̓_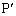 �ɂ��āA�O�p�`��2�ӂ̘a�͑���1�ӂ��傫���̂ŁA
�ɂ��āA�O�p�`��2�ӂ̘a�͑���1�ӂ��傫���̂ŁA �ƂȂ邩��ł��B
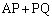 �̍ŏ��l�́A
�̍ŏ��l�́A 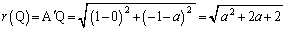 ......[��]
......[��](��) Q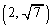 ��A�͒���
��A�͒���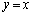 �̋t���ɂ���̂ŁA����Q�ɑ��āA
�̋t���ɂ���̂ŁA����Q�ɑ��āA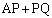 �̍ŏ��l�́A
�̍ŏ��l�́A 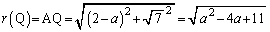 ......[��]
......[��]
(2)(i)(��) Q���A����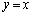 �������ɂ���A�܂�A�̈�
�������ɂ���A�܂�A�̈�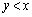 ���ɂ���Ƃ��A
���ɂ���Ƃ��A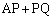 �̍ŏ��l��
�̍ŏ��l��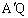 �ł��B
�ł��B �o�Ȑ�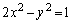 ��̓_��y���W��t (
��̓_��y���W��t (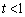 )�Ƃ���ƁAx���W��
)�Ƃ���ƁAx���W��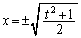 �ł��B
�ł��B 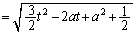
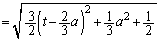 �@����@
�@����@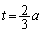 �̂Ƃ���
�̂Ƃ���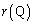 �ŏ��ƂȂ�܂����A
�ŏ��ƂȂ�܂����A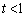 �Ȃ̂ŁA
�Ȃ̂ŁA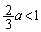 �C�܂�A
�C�܂�A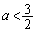 �ł���K�v������܂��B
�ł���K�v������܂��B
�̈�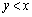 ���̓_Q
���̓_Q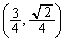 �ɂ�����
�ɂ�����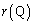 �ŏ��ƂȂ�̂́AQ��y���W�ɂ��āA
�ŏ��ƂȂ�̂́AQ��y���W�ɂ��āA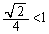 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA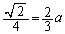 �C�܂�A
�C�܂�A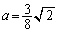 ......[��]�@�̂Ƃ��ł��B
......[��]�@�̂Ƃ��ł��B(��) Q���A����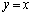 ������ɂ���A�܂�A�̈�
������ɂ���A�܂�A�̈�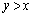 ���ɂ���Ƃ��A
���ɂ���Ƃ��A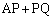 �̍ŏ��l��
�̍ŏ��l��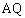 �ł��B
�ł��B �o�Ȑ�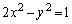 ��̓_��x���W��s (
��̓_��x���W��s (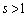 )�Ƃ���ƁAy���W��
)�Ƃ���ƁAy���W��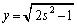 (
(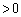 )�ł��B
)�ł��B 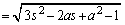
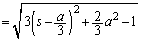 �@����A
�@����A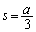 �̂Ƃ���
�̂Ƃ���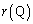 �ŏ��ƂȂ�܂����A
�ŏ��ƂȂ�܂����A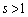 �Ȃ̂ŁA
�Ȃ̂ŁA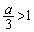 �C�܂�A
�C�܂�A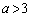 �ł���K�v������܂��B
�ł���K�v������܂��B
�̈�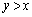 ���̓_Q
���̓_Q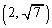 �ɂ�����
�ɂ�����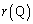 �ŏ��ƂȂ�̂́AQ��x���W�ɂ��āA
�ŏ��ƂȂ�̂́AQ��x���W�ɂ��āA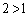 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA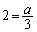 �C�܂�A
�C�܂�A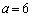 ......[��]�@�̂Ƃ��ł��B
......[��]�@�̂Ƃ��ł��B�@��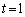 �C�A��
�C�A��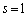 �Ƃ����Ƃ��ɂ��A
�Ƃ����Ƃ��ɂ��A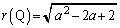 (
(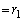 �Ƃ����܂�)�ƂȂ�܂��B(i)������ƁA
�Ƃ����܂�)�ƂȂ�܂��B(i)������ƁA �E�̈�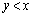 ���ɑ��݂���o�Ȑ���̓_�ɂ�����
���ɑ��݂���o�Ȑ���̓_�ɂ�����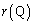 ���ŏ��l
���ŏ��l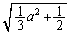 ���Ƃ�A
���Ƃ�A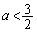
�E�̈�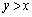 ���ɑ��݂���o�Ȑ���̓_�ɂ�����
���ɑ��݂���o�Ȑ���̓_�ɂ�����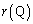 ���ŏ��l
���ŏ��l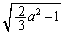 ���Ƃ�A
���Ƃ�A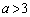
�Ƃ������ƂɂȂ�܂��B
����Ă��邱�Ƃɂ͒��ڊW���܂��A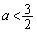 �̂Ƃ���
�̂Ƃ���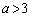 �̂Ƃ��ɂ���
�̂Ƃ��ɂ���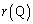 �ŏ����l���Ă݂܂��B
�ŏ����l���Ă݂܂��B (a) 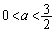 �̂Ƃ��A
�̂Ƃ��A �_Q���̈�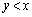 ���ɑ��݂���o�Ȑ�����Ƃ��A�@�ɂ�����
���ɑ��݂���o�Ȑ�����Ƃ��A�@�ɂ�����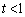 �͈̔͂�t�������̂ŁA
�͈̔͂�t�������̂ŁA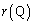 �́A
�́A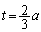 (
(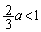 )�̂Ƃ��ŏ��l
)�̂Ƃ��ŏ��l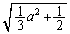 ���Ƃ�܂��B
���Ƃ�܂��B
�_Q���̈�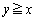 ���ɑ��݂���o�Ȑ�����Ƃ��A�A�ɂ�����
���ɑ��݂���o�Ȑ�����Ƃ��A�A�ɂ�����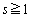 �͈̔͂�s�������̂ŁA
�͈̔͂�s�������̂ŁA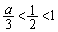 �ł��邱�Ƃ���
�ł��邱�Ƃ���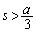 �ł�����
�ł�����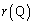 ��s�̑������ŁA
��s�̑������ŁA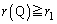 �ł��B
�ł��B
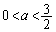 �ɂ����ẮA
�ɂ����ẮA ���A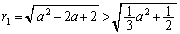 �Ȃ̂ŁAQ���o�Ȑ�
�Ȃ̂ŁAQ���o�Ȑ�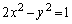 ��
��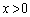 �̕������ƁA
�̕������ƁA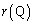 �́A
�́A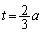 �̂Ƃ��ŏ��l
�̂Ƃ��ŏ��l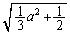 ���Ƃ�܂��B���̂Ƃ��AQ�͑o�Ȑ�C��
���Ƃ�܂��B���̂Ƃ��AQ�͑o�Ȑ�C��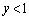 �̕����ɂ���܂��B
�̕����ɂ���܂��B (b) 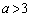 �̂Ƃ��A
�̂Ƃ��A �_Q���̈�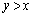 ���ɑ��݂���o�Ȑ�����Ƃ��A�A�ɂ�����
���ɑ��݂���o�Ȑ�����Ƃ��A�A�ɂ�����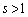 �͈̔͂�s�������̂ŁA
�͈̔͂�s�������̂ŁA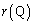 �́A
�́A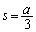 (
(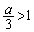 )�̂Ƃ��A�ŏ��l
)�̂Ƃ��A�ŏ��l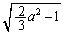 ���Ƃ�܂��B
���Ƃ�܂��B
�_Q���̈�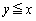 ���ɑ��݂���o�Ȑ�����Ƃ��A�@�ɂ�����
���ɑ��݂���o�Ȑ�����Ƃ��A�@�ɂ�����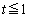 �͈̔͂�t�������̂ŁA
�͈̔͂�t�������̂ŁA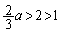 �ł��邱�Ƃ���
�ł��邱�Ƃ���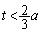 �ł�����
�ł�����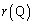 ��s�̌������ŁA
��s�̌������ŁA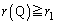 �ł��B
�ł��B
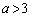 �ɂ����ẮA
�ɂ����ẮA ���A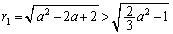 �Ȃ̂ŁAQ���o�Ȑ�
�Ȃ̂ŁAQ���o�Ȑ�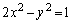 ��
��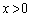 �̕������ƁA
�̕������ƁA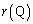 �́A
�́A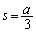 �̂Ƃ��ŏ��l
�̂Ƃ��ŏ��l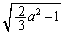 ���Ƃ�܂��B���̂Ƃ��AQ�͑o�Ȑ�C��
���Ƃ�܂��B���̂Ƃ��AQ�͑o�Ȑ�C��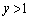 �̕����ɂ���܂��B
�̕����ɂ���܂��B (a)�C(b)���A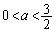 �C
�C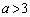 �̂Ƃ��ɂ́AQ�͑o�Ȑ�C��
�̂Ƃ��ɂ́AQ�͑o�Ȑ�C��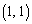 �ȊO�̓_��
�ȊO�̓_��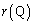 �ŏ��ƂȂ�܂��B
�ŏ��ƂȂ�܂��B
���āA(a)�C(b)�Ɠ��l�ɁA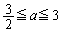 �̏ꍇ�ׂĂ݂܂��B�������ł͂��̏ꍇ�����l�����OK�ł��B
�̏ꍇ�ׂĂ݂܂��B�������ł͂��̏ꍇ�����l�����OK�ł��B
�_Q���̈�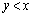 ���ɑ��݂���o�Ȑ�����Ƃ��A�@�ɂ�����
���ɑ��݂���o�Ȑ�����Ƃ��A�@�ɂ�����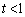 �͈̔͂�t�������̂ŁA
�͈̔͂�t�������̂ŁA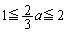 �ł��邱�Ƃ���
�ł��邱�Ƃ���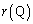 ��t�̌������ŁA
��t�̌������ŁA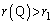
�_Q���̈�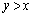 ���ɑ��݂���o�Ȑ�����Ƃ��A�A�ɂ�����
���ɑ��݂���o�Ȑ�����Ƃ��A�A�ɂ�����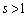 �͈̔͂�s�������̂ŁA
�͈̔͂�s�������̂ŁA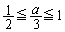 �ł��邱�Ƃ���
�ł��邱�Ƃ���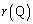 ��s�̑������ŁA
��s�̑������ŁA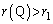
������A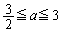 �̂Ƃ��ɁA
�̂Ƃ��ɁA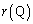 �́AQ��
�́AQ��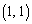 �ɗ����Ƃ��ɍŏ��ɂȂ�܂��B����āA
�ɗ����Ƃ��ɍŏ��ɂȂ�܂��B����āA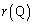 ��Q
��Q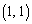 �ɂ����čŏ��l���Ƃ�悤��a�͈̔͂́A
�ɂ����čŏ��l���Ƃ�悤��a�͈̔͂́A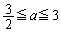 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B